【题目】已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有![]() ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
参考答案:
【答案】(1)0,2(2)减函数(3)(﹣2,1).
【解析】试题分析:(1)令x=y=0求f(0)=0;再令x=-y=1得f(0)=f(1)+f(-1);从而求解;(2)可判断函数f(x)是R上的减函数,利用定义证明;(3)由(2)知,f(2x)﹣f(x2+3x)<4可化为f(2x-x2-3x)<f(-2);从而得x2+x-2<0,从而解得
试题解析:(1)令x=y=0得,
f(0)=f(0)+f(0);
故f(0)=0;
令x=﹣y=1得,
f(0)=f(1)+f(﹣1);
故f(﹣1)=f(0)﹣f(1)=2; (3分)
(2)函数f(x)是R上的减函数,证明如下,
令x=﹣y得,f(0)=f(x)+f(﹣x);
故f(x)=﹣f(﹣x);
任取x1,x2∈R,且x1<x2,
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)
=f(x1﹣x2)=﹣f(x2﹣x1),
故由f(x2﹣x1)<0知,﹣f(x2﹣x1)>0,
从而得f(x1)﹣f(x2)>0,
则函数f(x)是R上的减函数; (4分)
(3)由(2)知,
f(2x)﹣f(x2+3x)<4可化为
f(2x﹣x2﹣3x)<f(﹣2);
故x2+x﹣2<0,
解得,x∈(﹣2,1). (5分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】通常表明地震能量大小的尺度是里氏震级,其计算公式为:
 ,其中,
,其中, 是被测地震的最大振幅,
是被测地震的最大振幅, 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差)。(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是30,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算8级地震的最大振幅是5级地震的最大振幅的多少倍?
(以下数据供参考:
 ,
,  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知随机变量X~N(μ,σ2),且其正态曲线在(-∞,80)上是增函数,在(80,+∞)上为减函数,且P(72≤X≤88)=0.682 6.
(1)求参数μ,σ的值;
(2)求P(64<X≤72).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
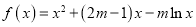 .
.(1)当
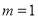 时, 求曲线
时, 求曲线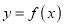 的极值;
的极值;(2)求函数
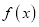 的单调区间;
的单调区间;(3)若对任意
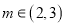 及
及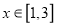 时, 恒有
时, 恒有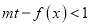 成立, 求实数
成立, 求实数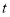 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
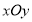 中,记二次函数
中,记二次函数 (
(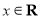 )与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为
)与两坐标轴有三个交点,其中与x轴的交点为A,B.经过三个交点的圆记为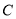 .
.(1)求圆
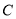 的方程;
的方程;(2)设P为圆
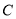 上一点,若直线PA,PB分别交直线
上一点,若直线PA,PB分别交直线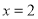 于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论.
于点M,N,则以MN为直径的圆是否经过线段AB上一定点?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】围建一个面积为360
 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为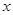 (单位:
(单位: ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为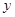 (单位:元)
(单位:元)
(1)将
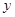 表示为
表示为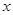 的函数;
的函数;(2)试确定
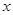 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设各项均为正数的数列
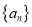 满足
满足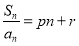 (
(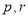 为常数),其中
为常数),其中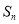 为数列
为数列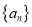 的前
的前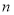 项和.
项和.(1)若
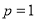 ,
,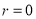 ,求证:
,求证: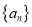 是等差数列;
是等差数列;(2)若
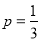 ,
,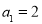 ,求数列
,求数列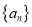 的通项公式;
的通项公式;(3)若
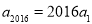 ,求
,求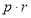 的值.
的值.
相关试题

