【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取n人进行问卷调查,把这n人按年龄分成5组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的样本的频率分布直方图如右:

调查问题是“双峰山国家森林公园是几A级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
参考答案:
【答案】(1)![]() ;(2)2人,3人,2人;(3)
;(2)2人,3人,2人;(3)![]() .
.
【解析】
(1)由频率分布直方图求出第1组的总人数,结合直方图,能求出n.
(2)由频率分布直方图得第2,3,4组的人数,再利用分层抽样的比例,求出各组抽取的人数.
(3)利用列举法列举出所有基本事件的个数,从中找到符合条件的个数,再利用古典概型公式计算概率.
(1)由频率表中第1组数据可知,第1组总人数为![]() 10.
10.
再结合频率分布直方图可知n![]() 100,
100,
所以x=![]() =0.9, y=100×0.03×10×0.9=27,
=0.9, y=100×0.03×10×0.9=27,
(2)因为第2,3,4组回答正确的共有54人,由频率分布直方图得第2组的人数为18,第3组的人数为27,第4组的人数为9,
所以利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组:![]() ×6=2;第3组:
×6=2;第3组:![]() ×6=3;第4组:
×6=3;第4组:![]() ×6=1.
×6=1.
(3)设第2组的2人为A1,A2;第3组的3人为B1,B2,B3;第4组的1人为C1.
则从6人中随机抽取2人的所有可能的结果为:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,B2),(B1,B3),(B1,C1),(B2,B3),(B2,C1),(B3,C1),共15种,
其中所抽取的两人来自不同组的结果为:
(A1,B1),(A1,B2),(A1,B3),(A1,C1),(A2,B1),(A2,B2),(A2,B3),(A2,C1),(B1,C1), (B2,C1),(B3,C1),共11种,
所以所抽取的两人来自不同年龄组概率P=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起,设折起后点A的位置为A′,使二面角A′—BD—C为直二面角,给出下面四个命题:①A′D⊥BC;②三棱锥A′—BCD的体积为
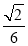 ;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )
;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明
 是等比数列,并求{an}的通项公式;
是等比数列,并求{an}的通项公式;(2)证明:
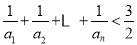 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(-2,1),
=(-2,1), =(x,y).
=(x,y).(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
 的概率;
的概率;(2)若x,y在区间[1,6]内取值,求满足
 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为
 ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别 ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
 ,求
,求 的分布列与数学期望
的分布列与数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地随着经济的发展,居民收入逐年增长,经统计知年份x和储蓄
存款y (千亿元)具有线性相关关系,下表是该地某银行连续五年的储蓄存款(年底余额),
如下表(1):
年份x
2014
2015
2016
2017
2018
储蓄存款y(千亿元)
5
6
7
8
10
表(1)
为了研究计算的方便,工作人员将上表的数据进行了处理,令

得到下表(2):
时间代号t
1
2
3
4
5

0
1
2
3
5
表(2)
(1)由最小二乘法求
 关于t的线性回归方程;
关于t的线性回归方程;(2)通过(1)中的方程,求出y关于x的线性回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线
 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.

(1)从服药的50名患者中随机选出一人,求此人指标x的值小于1.7的概率;
(2)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
(3)若指标x小于1.7且指标y大于60就说总生理指标正常(例如图中B、D两名患者的总生理指标正常),根据上图,完成下面
 列联表,并判断能否有95%的把握认为总生理指标正常与是否服药有关,说明理由;
列联表,并判断能否有95%的把握认为总生理指标正常与是否服药有关,说明理由;总生理指标正常
总生理指标不正常
总计
服药
不服药
总计
P(K2≥k0)
0.10
0.05
0.010
0.005
k0
2.706
3.841
6.635
7.879
附:

相关试题

