【题目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(2cosx,1).
=(2cosx,1).
(1)若 ![]() ∥
∥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() ⊥
⊥ ![]() ,又x∈[π,2π],求sinx+cosx的值.
,又x∈[π,2π],求sinx+cosx的值.
参考答案:
【答案】
(1)解:由a∥b,得sinx1﹣2cosx(﹣1)=0,即sinx=﹣2cosx,
所以tanx=﹣2;
(2)解:由a⊥b,得sinx2cosx+1(﹣1)=0,即2sinxcosx=1,
又x∈[π,2π],所以sinx<0,cosx<0,即sinx+cosx<0
因为(sinx+cosx)2=sin2x+2sinxcosx+cos2x…(10分)=1+2sinxcosx=2,
则 ![]()
【解析】(1)根据向量的平行的条件和同角的三角函数的关系即可求出;(2)根据向量的垂直的条件和同角的平方关系即可求出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
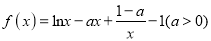
(1)设
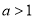 ,试讨论
,试讨论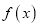 单调性;
单调性;(2)设
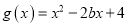 ,当
,当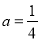 时,任意
时,任意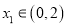 ,存在
,存在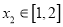 ,使
,使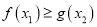 ,求实数
,求实数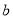 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知中心在原点,焦点在
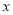 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为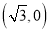 ,
, 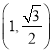 是椭圆上的一个点.
是椭圆上的一个点.(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为
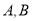 ,
, 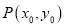 (
(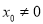 )是椭圆上异于
)是椭圆上异于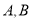 的任意一点,
的任意一点, 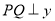 轴,
轴, 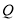 为垂足,
为垂足, 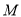 为线段
为线段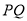 中点,直线
中点,直线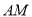 交直线
交直线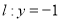 于点
于点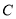 ,
, 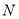 为线段
为线段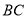 的中点,如果
的中点,如果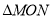 的面积为
的面积为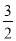 ,求
,求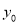 的值.
的值.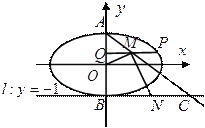
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移  个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点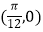 对称
对称
B.关于点 对称
对称
C.关于直线 对称
对称
D.关于直线 对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线 l1和l2 是异面直线,l1在平面 α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( )
A.l与l1 , l2都不相交
B.l与l1 , l2都相交
C.l至多与l1 , l2中的一条相交
D.l至少与l1 , l2中的一条相交 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(π﹣2x),g(x)=2cos2x,则下列结论正确的是( )
A.函数f(x)在区间[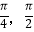 ]上为增函数
]上为增函数
B.函数y=f(x)+g(x)的最小正周期为2π
C.函数y=f(x)+g(x)的图象关于直线x= 对称
对称
D.将函数f(x)的图象向右平移 个单位,再向上平移1个单位,得到函数g(x)的图象
个单位,再向上平移1个单位,得到函数g(x)的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,BC=DC=AB=AD=
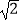 ,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 .
,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P﹣QCO体积的最大值为 . 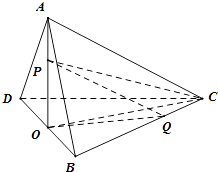
相关试题

