【题目】f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,则方程f(x)﹣f′(x)=e的实数解所在的区间是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(1,e)
D.(e,3)
参考答案:
【答案】C
【解析】解:∵f(x)是定义在(0,+∞)上单调函数,且对x∈(0,+∞),都有f(f(x)﹣lnx)=e+1,
∴设f(x)﹣lnx=t,则f(t)=e+1,
即f(x)=lnx+t,
令x=t,则f(t)=lnt+t=e+1,
则t=e,
即f(x)=lnx+e,
函数的导数f′(x)= ![]() ,
,
则由f(x)﹣f′(x)=e得lnx+e﹣ ![]() =e,
=e,
即lnx﹣ ![]() =0,
=0,
设h(x)=lnx﹣ ![]() ,
,
则h(1)=ln1﹣1=﹣1<0,h(e)=lne﹣ ![]() =1﹣
=1﹣ ![]() >0,
>0,
∴函数h(x)在(1,e)上存在一个零点,即方程f(x)﹣f′(x)=e的实数解所在的区间是(1,e),
故选:C.
利用换元法求出函数f(x)的解析式,然后根据函数与方程的关系进行转化,构造函数,判断函数的零点即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线E:y2=2px(p>0)的准线与x轴交于点K,过点K作圆(x﹣5)2+y2=9的两条切线,切点为M,N,|MN|=3

(1)求抛物线E的方程;
(2)设A,B是抛物线E上分别位于x轴两侧的两个动点,且 (其中O为坐标原点).
(其中O为坐标原点).
①求证:直线AB必过定点,并求出该定点Q的坐标;
②过点Q作AB的垂线与抛物线交于G,D两点,求四边形AGBD面积的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求过点
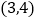 且与两坐标轴截距相等的直线
且与两坐标轴截距相等的直线 的方程;
的方程;(2)已知正方形
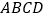 的中心为直线
的中心为直线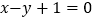 和直线
和直线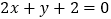 的交点,且
的交点,且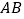 边所在直线方程为
边所在直线方程为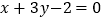 ,求
,求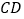 边所在直线的方程.
边所在直线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】运行如图所示的程序框图,则输出的结果是( )

A.e2016﹣e2015
B.e2017﹣e2016
C.e2015﹣1
D.e2016﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ;②y=
;②y=  ;③y=
;③y=  ;④y=
;④y=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形的中心为直线
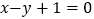 和直线
和直线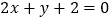 的交点,其一边所在直线方程为
的交点,其一边所在直线方程为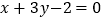
(1)写出正方形的中心坐标;
(2)求其它三边所在直线的方程(写出一般式).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知椭圆
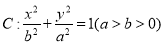 的离心率为
的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.(1)求椭圆C的方程;
(2)已知直线
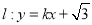 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
相关试题

