【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
参考答案:
【答案】(1)f(x)=20×![]() +6x=
+6x=![]() +6x(0≤x≤10)(2)5 cm厚,70万元
+6x(0≤x≤10)(2)5 cm厚,70万元
【解析】试题分析:(1)由C(x)=![]() ,可先求出k的值(C(0)=8),然后根据题意;f(x)为隔热层建造费用与20年的能源消耗费用之和,即6x(隔热层建造费用)+20×
,可先求出k的值(C(0)=8),然后根据题意;f(x)为隔热层建造费用与20年的能源消耗费用之和,即6x(隔热层建造费用)+20×![]() (20年的能源消耗费);
(20年的能源消耗费);
(2)由(1)已知函数解析式,可转化为求函数的最值,可运用导数可求出最值。(注意定义域)
试题解析:(1)设隔热层厚度为x cm,由题设,每年能源消耗费用为C(x)=![]() ,
,
再由C(0)=8,得k=40,因此C(x)=![]() ,而建造费用为C1(x)=6x.
,而建造费用为C1(x)=6x.
最后得隔热层建造费用与20年的能源消耗费用之和为
f(x)=20C(x)+C1(x)=20×![]() +6x=
+6x=![]() +6x(0≤x≤10).
+6x(0≤x≤10).
(2)f ′(x)=6-![]() ,
,
令f ′(x)=0,即![]() =6,解得x=5,x=-
=6,解得x=5,x=-![]() (舍去).
(舍去).
当0<x<5时,f ′(x)<0, 当5<x<10时,f ′(x)>0,
故x=5是f(x)的最小值点,对应的最小值为f(5)=6×5+![]() =70.
=70.
当隔热层修建5 cm厚时,总费用达到最小值70万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
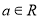 ,函数
,函数 .
.(1)求证:曲线
 在点
在点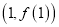 处的切线过定点;
处的切线过定点;(2)若
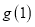 是
是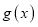 在区间
在区间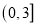 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数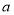 的取值范围;
的取值范围;(3)求证:对任意给定的正数
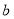 ,总存在
,总存在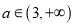 ,使得
,使得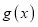 在
在 上为单调函数.
上为单调函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中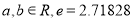 是自然对数的底数.
是自然对数的底数.(1)若曲线
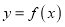 在
在 处的切线方程为
处的切线方程为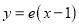 .求实数
.求实数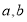 的值;
的值;(2)①若
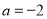 时,函数
时,函数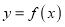 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数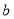 的取值范围;
的取值范围;②若
 ,若
,若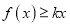 对一切正实数
对一切正实数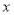 恒成立,求实数
恒成立,求实数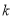 的取值范围(用
的取值范围(用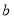 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为
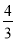 ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.(Ⅰ)根据题意建立的
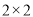 列联表,并判断是否有
列联表,并判断是否有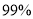 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
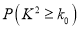
0.100
0.050
0.010
0.001
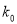
2.706
3.841
6.635
10.828
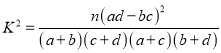 ,
, 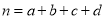 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)当
 时,若
时,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)设函数
 的图象在两点
的图象在两点 处的切线分别为
处的切线分别为 ,若
,若 ,且
,且 ,求实数
,求实数 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段
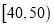 ,
, 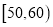 …
…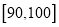 后画出如下频率分布直方图.观察图形的信息,回答下列问题:
后画出如下频率分布直方图.观察图形的信息,回答下列问题: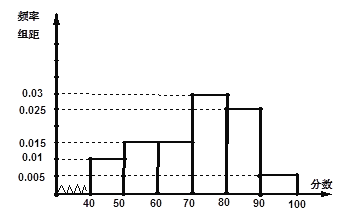
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
相关试题

