【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为 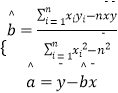 .
.
参考答案:
【答案】
(1)解: ![]() =
= ![]() =4.5,
=4.5, ![]() =
= ![]() =3.5,
=3.5,
![]() =3×2.5+4×3+5×4+6×4.5=66.5,
=3×2.5+4×3+5×4+6×4.5=66.5,
![]() =32+42+52+62=86,
=32+42+52+62=86,
∴ ![]() =
= 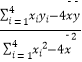 =
= ![]() =0.7,
=0.7,
![]() =3.5﹣0.7×4.5=0.35.
=3.5﹣0.7×4.5=0.35.
∴所求的回归方程为 ![]() =0.7x+0.35
=0.7x+0.35
(2)解:现在生产100吨甲产品用煤
![]() =0.7×100+0.35=70.35,∴90﹣70.35=19.65.
=0.7×100+0.35=70.35,∴90﹣70.35=19.65.
∴生产能耗比技改前降低约19.65吨标准煤
【解析】(1)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.(2)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低标准煤的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中,bn>0(n∈N*),且b1+b2+b3=15,又a1+b1、a2+b2、a3+b3成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)求数列{an·bn}的前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩
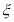 服从正态分布
服从正态分布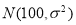 ,已知
,已知 ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取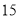 份;
份;②已知命题
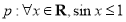 ,则
,则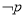 :
: ;
;③在
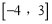 上随机取一个数
上随机取一个数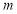 ,能使函数
,能使函数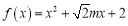 在
在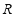 上有零点的概率为
上有零点的概率为 ;
;④设
 ,则“
,则“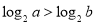 ”是“
”是“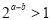 ”的充要条件.
”的充要条件.其中真命题的序号为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线
 的极坐标方程是
的极坐标方程是 ,以极点为原点
,以极点为原点 ,极轴为
,极轴为 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: (
( 为参数).
为参数).(1)求曲线
 的直角坐标方程与曲线
的直角坐标方程与曲线 的普通方程;
的普通方程;(2)将曲线
 经过伸缩变换
经过伸缩变换 后得到曲线
后得到曲线 ,若
,若 分别是曲线
分别是曲线 和曲线
和曲线 上的动点,求
上的动点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用.出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天
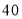 名读书者进行调查,将他们的年龄分成6段:
名读书者进行调查,将他们的年龄分成6段: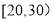 ,
,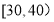 ,
,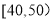 ,
,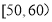 ,
,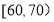 ,
,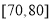 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:(1)估计在40名读书者中年龄分布在
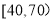 的人数;
的人数;(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在
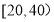 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在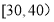 的人数
的人数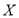 的分布列及数学期望.
的分布列及数学期望.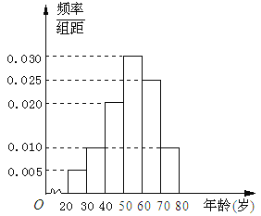
-
科目: 来源: 题型:
查看答案和解析>>【题目】静宁县是甘肃苹果栽培第一大县,中国著名优质苹果基地和重要苹果出口基地.静宁县海拔高、光照充足、昼夜温差大、环境无污染,适合种植苹果.“静宁苹果”以色泽鲜艳、质细汁多,酸甜适度,口感脆甜、货架期长、极耐储藏和长途运输而著名.为检测一批静宁苹果,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量)
[80,85)
[85,90)
[90,95)
[95,100)
频数(个)
5
10
20
15
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个.甲、乙二人依次各抽一题.
(1)甲抽到选择题、乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一人抽到选择题的概率是多少?
相关试题

