《2025年学生基础性作业三年级数学上册北师大版》

4 评价
时长 分钟
课时3 买文具(1)
一、轻松算吧。
$58-34= $24
$81÷9= $9
$72-24÷4= $66
$35÷7+24= $29
$42+54= $96
$48÷6= $8
$36÷4+36= $45
$63-25÷5= $58

答案： 1. $58 - 34 = 24$
2. $81÷9 = 9$
3.
$72 - 24÷4$
$=72 - 6$
$= 66$
4.
$35÷7 + 24$
$= 5 + 24$
$= 29$
5. $42 + 54 = 96$
6. $48÷6 = 8$
7.
$36÷4 + 36$
$= 9 + 36$
$= 45$
8.
$63 - 25÷5$
$= 63 - 5$
$= 58$

1. 把下面每组中的两道算式合并成一道综合算式。
(1)$63÷7= 9$ $9+25= 34$ $63÷7 + 25=34$
(2)$19-8= 11$ $64÷8= 8$ $19-64÷8 = 11$
(3)$16÷8= 2$ $76-2= 74$ $76-16÷8 = 74$
(4)$22-9= 13$ $63÷7= 9$ $22-63÷7 = 13$

答案： 1. （1）
解：第一个式子的结果$9$是第二个式子的加数，所以综合算式为$63÷7 + 25$
计算$63÷7+25=9 + 25=34$，综合算式为$63÷7 + 25=34$。
2. （2）
解：第二个式子的结果$8$是第一个式子的减数，所以综合算式为$19-64÷8$
计算$19 - 64÷8=19 - 8=11$，综合算式为$19-64÷8 = 11$。
3. （3）
解：第一个式子的结果$2$是第二个式子的减数，所以综合算式为$76-16÷8$
计算$76-16÷8=76 - 2=74$，综合算式为$76-16÷8 = 74$。
4. （4）
解：第二个式子的结果$9$是第一个式子的减数，所以综合算式为$22-63÷7$
计算$22-63÷7=22 - 9=13$，综合算式为$22-63÷7 = 13$。
故答案依次为：（1）$63÷7 + 25=34$；（2）$19-64÷8 = 11$；（3）$76-16÷8 = 74$；（4）$22-63÷7 = 13$。

2. 淘气每天比笑笑少看多少页？

答案： 1. 淘气每天看的页数：45÷5=9（页）
2. 淘气每天比笑笑少看的页数：11-9=2（页）
答：淘气每天比笑笑少看2页。

3. 一副乒乓球拍比一个羽毛球贵多少元？

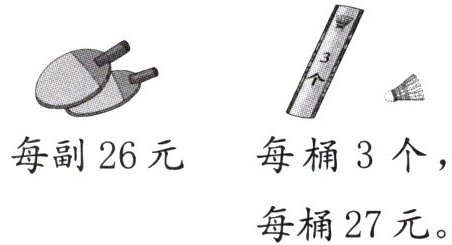
答案： 1. 首先求一个羽毛球的价格：
已知每桶羽毛球$3$个，每桶$27$元，根据“单价 = 总价÷数量”，可得一个羽毛球的价格为$27÷3 = 9$（元）。
2. 然后求一副乒乓球拍比一个羽毛球贵的金额：
已知一副乒乓球拍$26$元，一个羽毛球$9$元，所以一副乒乓球拍比一个羽毛球贵$26 - 9=17$（元）。
答：一副乒乓球拍比一个羽毛球贵$17$元。

三、妙想实践。
有16名教师要开会,会议室现在有9把双人椅,所有教师坐好后(按顺序依次紧挨着坐),还剩多少把双人椅？

答案： 1. 计算16名教师需要的双人椅数量：16÷2=8（把）
2. 计算剩余双人椅数量：9-8=1（把）
答：还剩1把双人椅。