第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
4. 量出下面各角的度数。
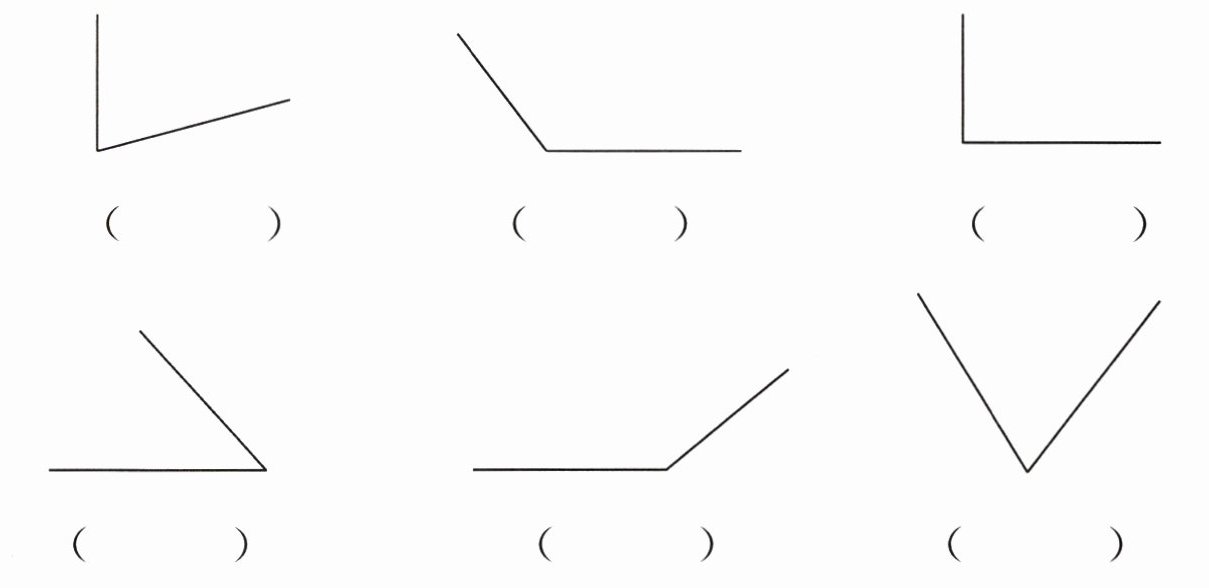
75° 130° 90°
50° 140° 70°

75° 130° 90°
50° 140° 70°
答案:
75° 130° 90°
50° 140° 70°
50° 140° 70°
5. 先量出下面各角的度数,再算一算,你发现了什么?
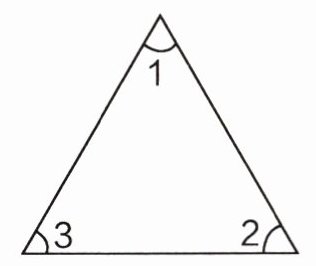
$∠1 = ($
$∠3 = ($

$∠1 = ($
$∠3 = ($
我发现:

$∠1 = ($
60°
) $∠2 = ($60°
)$∠3 = ($
60°
) $∠1 + ∠2 + ∠3 = ($180°
)
$∠1 = ($
60°
) $∠2 = ($30°
)$∠3 = ($
90°
) $∠1 + ∠2 + ∠3 = ($180°
)我发现:
三角形三个角的度数和是180°。
答案:
60° 60° 60° 180° 60° 30° 90° 180° 我发现:三角形三个角的度数和是180°。
6. 数一数,一共有多少个角?发现什么规律了吗?
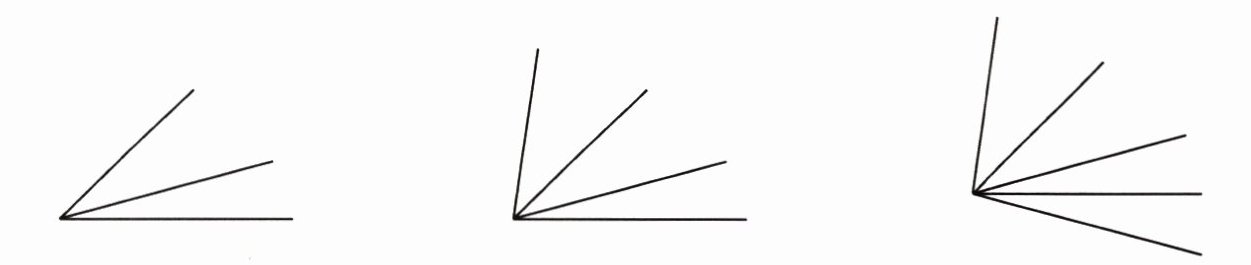

答案:
3 6 10 规律:当一个顶点引出$n$条射线时,角的总个数为$1+2+3+\cdots+(n-1)=\frac{n(n-1)}{2}$。
$240÷8 = $
$257 + 298 = $
$0.9 + 1.1 = $
$420÷7 = $
$100 - 60 = $
$750 + 50 = $
$50×11 = $
$261 - 199 = $
30
$257 + 298 = $
555
$0.9 + 1.1 = $
2.0
$420÷7 = $
60
$100 - 60 = $
40
$750 + 50 = $
800
$50×11 = $
550
$261 - 199 = $
62
答案:
$240÷8 = 30$
$257 + 298 = 555$
$0.9 + 1.1 = 2.0$
$420÷7 = 60$
$100 - 60 = 40$
$750 + 50 = 800$
$50×11 = 550$
$261 - 199 = 62$
$257 + 298 = 555$
$0.9 + 1.1 = 2.0$
$420÷7 = 60$
$100 - 60 = 40$
$750 + 50 = 800$
$50×11 = 550$
$261 - 199 = 62$
查看更多完整答案,请扫码查看


