《2025年绩优学案一年级数学上册北师大版》

1. 数一数,填一填。

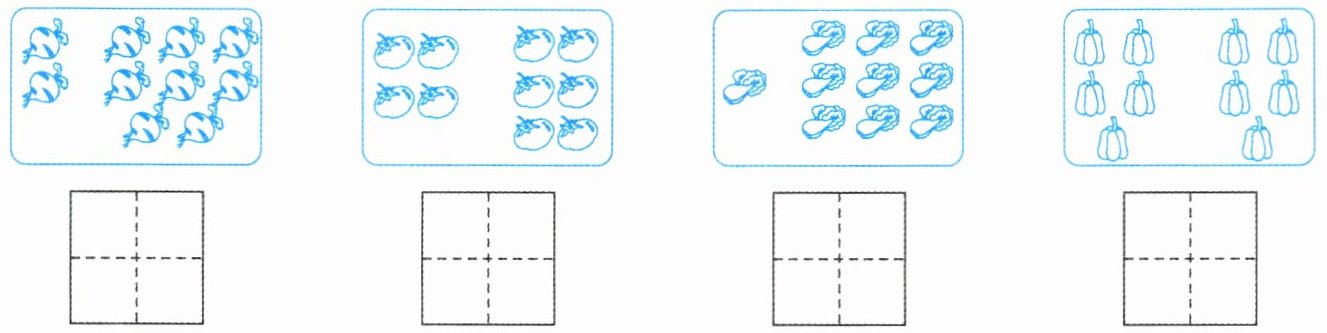
10,10,10,10

答案： 10,10,10,10

2. 根据下面的数,把缺少的图形画出来。

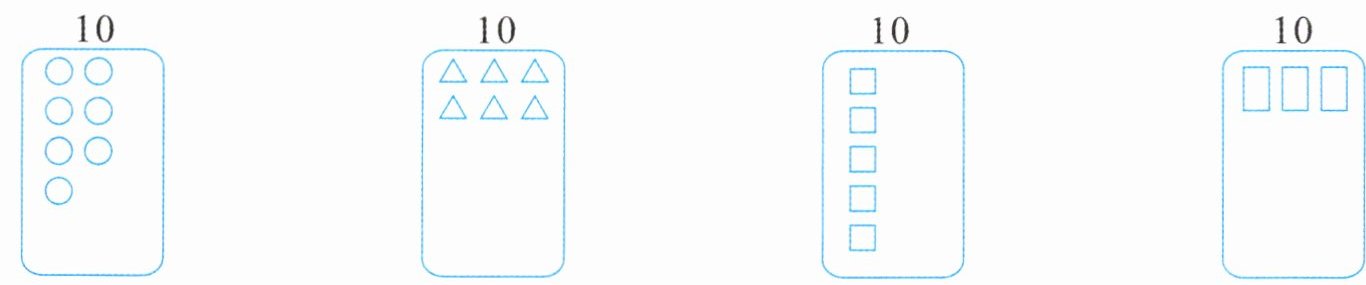
答案： 本题可先分析每个图形中已有的图形数量，再结合总数$10$计算出缺少的图形数量，最后画出缺少的图形。
- **第一个图形：
已知该图形中已有$7$个$◯$，总数是$10$，则缺少的$◯$数量为$10 - 7=3$（个）。
- **第二个图形：
已知该图形中已有$6$个$\triangle$，总数是$10$，则缺少的$\triangle$数量为$10 - 6 = 4$（个）。
- **第三个图形：
已知该图形中已有$6$个$□$，总数是$10$，则缺少的$□$数量为$10 - 6 = 4$（个）。
- **第四个图形：
已知该图形中已有$3$个$□$（此处根据图形推测是$□$，与前面图形规律统一），总数是$10$，则缺少的$□$数量为$10 - 3 = 7$（个）。
按照上述计算结果，补全图形如下：
第一个图形补$◯◯◯$；第二个图形补$\triangle\triangle\triangle\triangle$；第三个图形补$□□□□$；第四个图形补$□□□□□□□$。
故答案依次为：$\boldsymbol{◯◯◯}$；$\boldsymbol{\triangle\triangle\triangle\triangle}$；$\boldsymbol{□□□□}$；$\boldsymbol{□□□□□□□}$ 。

3. 想一想,画一画。

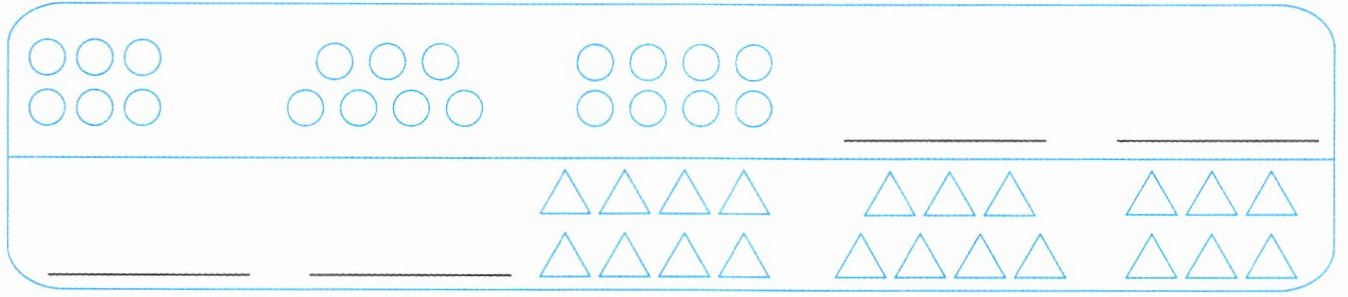
第一组圆有6个，第二组圆有7个，第三组圆有8个，按此规律，第四组应画9个圆，即○○○○○○○○○；第五组应画10个圆，即○○○○○○○○○○。
第一组三角形有8个，第二组三角形有7个，第三组三角形有6个，按此规律，第四组应画5个三角形，即△△△△△。

答案： 第一组圆有6个，第二组圆有7个，第三组圆有8个，按此规律，第四组应画9个圆，即○○○○○○○○○；第五组应画10个圆，即○○○○○○○○○○。
第一组三角形有8个，第二组三角形有7个，第三组三角形有6个，按此规律，第四组应画5个三角形，即△△△△△。

4. 谁更靠近餐车？画“√”。

解：小猫在1号车厢，餐车在6号车厢，它们之间间隔$6 - 1 = 5$个车厢。
小猴在10号车厢，餐车在6号车厢，它们之间间隔$10 - 6 = 4$个车厢。
因为$4\lt5$，所以小猴更靠近餐车，在小猴对应的方框画“√”。

答案： 解：小猫在1号车厢，餐车在6号车厢，它们之间间隔$6 - 1 = 5$个车厢。
小猴在10号车厢，餐车在6号车厢，它们之间间隔$10 - 6 = 4$个车厢。
因为$4\lt5$，所以小猴更靠近餐车，在小猴对应的方框画“√”。

5. 一共有(10)只鸭子。

答案： 10