第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
10. 小刚想找一种隔音效果好的材料,避免自己在听音乐时影响他人休息. 他身边有衣服、锡箔纸、泡沫塑料(他家的音箱太大,拿来做实验不太合适),可利用的器材还有音叉、机械闹钟、鞋盒.
(1)在本实验中,适合作声源的是
(2)小明将声源放入鞋盒内,在其四周塞满待测材料. 他设想下列两种实验方案,你认为最佳的是
A. 让人站在距鞋盒一定距离处,比较所听声音的响度
B. 让人一边听声音,一边向后退,直至听不见声音为止,比较此处到鞋盒的距离
实验得到的现象如表格所示,则待测材料隔声性能由好到差的顺序为
| 材料 | 衣服 | 锡箔纸 | 泡沫塑料 |
| 距离 | 较长 | 长 | 短 |
| 响度 | 较响 | 响 | 弱 |

(1)在本实验中,适合作声源的是
机械闹钟
.(2)小明将声源放入鞋盒内,在其四周塞满待测材料. 他设想下列两种实验方案,你认为最佳的是
B
.A. 让人站在距鞋盒一定距离处,比较所听声音的响度
B. 让人一边听声音,一边向后退,直至听不见声音为止,比较此处到鞋盒的距离
实验得到的现象如表格所示,则待测材料隔声性能由好到差的顺序为
泡沫塑料、衣服、锡箔纸
.| 材料 | 衣服 | 锡箔纸 | 泡沫塑料 |
| 距离 | 较长 | 长 | 短 |
| 响度 | 较响 | 响 | 弱 |

答案:
(1)机械闹钟
(2)B
泡沫塑料、衣服、锡箔纸
(1)机械闹钟
(2)B
泡沫塑料、衣服、锡箔纸
11. 探究影响音调高低的因素.
如图所示,让钢尺伸出桌边的长度不同,分别拨动钢尺,观察钢尺振动的快慢,听音调高低. 结果发现:钢尺伸出桌边越短,振动越
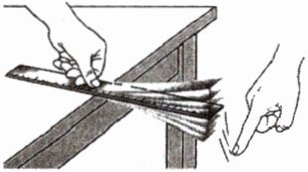
如图所示,让钢尺伸出桌边的长度不同,分别拨动钢尺,观察钢尺振动的快慢,听音调高低. 结果发现:钢尺伸出桌边越短,振动越
快
,发声的音调越高
. 说明物体振动越快,即频率
越高,音调越高.
答案:
快;高;频率
12. 利用超声波可以探测海洋的深度. 在一次测量中,从海面向海底发出超声波 $8$ s 后收到回声,则此处海底深度是多少米?(声波在海水中的传播速度是 $1.5 × 10^{3}$ m/s.)
答案:
已知:超声波从海面向海底发出到收到回声的时间$ t = 8\ s $,声波在海水中的传播速度$ v = 1.5× 10^{3}\ m/s $。
求:此处海底深度$ s $。
解:超声波从海面到海底再返回海面,传播的总路程为$ 2s $。
根据公式$ v=\frac{s_{总}}{t} $,可得$ s_{总}=vt $。
则$ 2s = vt $,$ s=\frac{vt}{2} $。
代入数据:$ s=\frac{1.5× 10^{3}\ m/s×8\ s}{2}=6× 10^{3}\ m $。
答:此处海底深度是$ 6× 10^{3}\ m $。
求:此处海底深度$ s $。
解:超声波从海面到海底再返回海面,传播的总路程为$ 2s $。
根据公式$ v=\frac{s_{总}}{t} $,可得$ s_{总}=vt $。
则$ 2s = vt $,$ s=\frac{vt}{2} $。
代入数据:$ s=\frac{1.5× 10^{3}\ m/s×8\ s}{2}=6× 10^{3}\ m $。
答:此处海底深度是$ 6× 10^{3}\ m $。
13. 某同学乘坐的汽艇遥对一座高崖,他向高崖大喊一声,经过 $5$ s 听到回声. 已知声速为 $340$ m/s,问:
(1)若汽艇静泊在水面,他离高崖有多远?
(2)若汽艇以 $10$ m/s 的速度正对高崖驶去,他大喊时离高崖有多远?
(1)若汽艇静泊在水面,他离高崖有多远?
(2)若汽艇以 $10$ m/s 的速度正对高崖驶去,他大喊时离高崖有多远?
答案:
(1)设他离高崖的距离为$s$,
根据速度公式$s = vt$,在$t = \frac{5}{2}s = 2.5s$(回声传播单程时间)内,声音传播的距离为:
$s = 340 × 2.5 = 850m$
答:他离高崖的距离为$850m$。
(2)设他大喊时离高崖的距离为$s^{\prime }$,
在$5s$内,汽艇行驶的距离:
$s_{1} = v_{1}t = 10 × 5 = 50m$,
声音传播的距离:
$s_{2} = v_{2}t = 340 × 5 = 1700m$,
由几何关系,有:
$2s^{\prime } = s_{1} + s_{2}$,
即:
$2s^{\prime } = 50 + 1700 = 1750m$,
解得:
$s^{\prime } = 875m$。
答:他大喊时离高崖的距离为$875m$。
(1)设他离高崖的距离为$s$,
根据速度公式$s = vt$,在$t = \frac{5}{2}s = 2.5s$(回声传播单程时间)内,声音传播的距离为:
$s = 340 × 2.5 = 850m$
答:他离高崖的距离为$850m$。
(2)设他大喊时离高崖的距离为$s^{\prime }$,
在$5s$内,汽艇行驶的距离:
$s_{1} = v_{1}t = 10 × 5 = 50m$,
声音传播的距离:
$s_{2} = v_{2}t = 340 × 5 = 1700m$,
由几何关系,有:
$2s^{\prime } = s_{1} + s_{2}$,
即:
$2s^{\prime } = 50 + 1700 = 1750m$,
解得:
$s^{\prime } = 875m$。
答:他大喊时离高崖的距离为$875m$。
查看更多完整答案,请扫码查看


