搜索
9. 数轴上点P表示的数为-3,与点P距离为4个单位长度的点表示的数为(
A.1
B.-7
C.1或-7
D.1或7
C
)A.1
B.-7
C.1或-7
D.1或7
答案：
C
10.(2024秋·玄武区月考)等边三角形ABC在数轴上的位置如图所示,点A,C对应的数分别为0和-1.若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转若干次后,数2025对应的点为(
A.点A
B.点B
C.点C
D.不确定
A
)A.点A
B.点B
C.点C
D.不确定
答案：
A
11. 计算：$|-2025|=$
2025
.
答案：
2025
12.(2024秋·大兴区期中)比较大小：$-\frac{3}{7}$
＞
$-\frac{2}{3}$.(填“＞”“＜”或“=”)
答案：
＞
13. 数轴上表示-1.2的点与表示2.5的点之间有
4
个整数点.
答案：
4
14. 已知$|2-a|= a-2$,请写一个满足条件的a的值：
2
.
答案：
2(答案不唯一)
15. 当x=
2
时,式子$|x-2|+2027$有最小值.
答案：
2
16. 若$|m-2|+|n-4|= 0$,则$m+n=$
6
.
答案：
6
17.(2024秋·南开区期中)在数轴上,点A表示的数是-5,从点A出发,沿数轴移动6个单位长度到达点B,则点B所表示的数为
1或−11
.
答案：
1或−11
18. 数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为1752.1厘米的线段AB,则线段AB能盖住的整点的个数是
1752或1753
.
答案：
1752或1753
19.(12分)把下列各数分别填入它们所属的集合内：
$-4,-|-\frac{4}{3}|,0,\frac{22}{7},-3.14,2023,-(+5),+1.88$.
(1)正数集合：{
(2)负数集合：{
(3)整数集合：{
$-4,-|-\frac{4}{3}|,0,\frac{22}{7},-3.14,2023,-(+5),+1.88$.
(1)正数集合：{
$\dfrac{22}{7},2023,+1.88$
···}；(2)负数集合：{
$-4,-\left\lvert -\dfrac{4}{3}\right\rvert,-3.14,-(+5)$
···}；(3)整数集合：{
$-4,0,2023,-(+5)$
···}.
答案：
解:
(1)正数集合：$\left\lbrace \dfrac{22}{7},2023,+1.88,\cdots\right\rbrace$；
(2)负数集合：$\left\lbrace -4,-\left\lvert -\dfrac{4}{3}\right\rvert,-3.14,-(+5),\cdots\right\rbrace$；
(3)整数集合：$\left\lbrace -4,0,2023,-(+5),\cdots\right\rbrace$．
(1)正数集合：$\left\lbrace \dfrac{22}{7},2023,+1.88,\cdots\right\rbrace$；
(2)负数集合：$\left\lbrace -4,-\left\lvert -\dfrac{4}{3}\right\rvert,-3.14,-(+5),\cdots\right\rbrace$；
(3)整数集合：$\left\lbrace -4,0,2023,-(+5),\cdots\right\rbrace$．
20.(8分)在数轴上表示下列各数：$0,-3,-1\frac{1}{3},2.5$,并按从小到大的顺序用“＜”把这些数连接起来.
答案：
解:如答图所示.
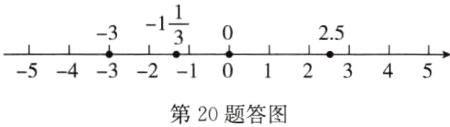故$-3＜-1\dfrac{1}{3}＜0＜2.5$．
解:如答图所示.
故$-3＜-1\dfrac{1}{3}＜0＜2.5$． 查看更多完整答案，请扫码查看
