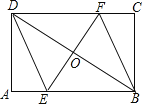
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
参考答案:
【答案】(1)证明见解析.(2)![]() .
.
【解析】
试题分析:(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
试题解析:(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
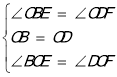 ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE⊥EF,
设BE=x,则 DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=![]() ,
,
∵BD=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∵BD⊥EF,
∴EO=![]() ,
,
∴EF=2EO=![]() .
.
-
科目: 来源: 题型:
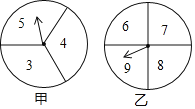
查看答案和解析>>【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a <0,则点P(-a,2)应在( )
A. 第一象限内 B. 第二象限内 C. 第三象限内 D. 第四象限内
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2和y﹣2互为相反数,求x+y的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式0□1=﹣1成立,则□内的运算符号为( )
A.+
B.﹣
C.×
D.÷ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列尺规作图的语句错误的是( )
A.作∠AOB,使∠AOB=3∠αB.作线段AB,使线段AB=a
C.以点O为圆心画弧D.作∠ABC,使∠ABC=∠α+∠β
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则|a+2|-|1-a|=________.
相关试题

