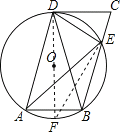
【题目】如图,在ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.

(1)求证:DE=DC;
(2)求证:直线DC是⊙O的切线.
参考答案:
【答案】见解析
【解析】
试题分析:(1)由平行四边形的性质得出AD∥BC,AB=DC,进而证得∠DAE=∠AEB,证出![]() =
=![]() ,即可得出DE=DC;
,即可得出DE=DC;
(2)作直径DF,连接EF,则∠EFD=∠EAD,证出∠EFD=∠CDE,再由DF是⊙O的直径,得出∠DEF=90°,得出∠FDC=90°,即可得出结论.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=DC,
∴∠DAE=∠AEB.
∴![]() =
=![]() ,
,
∴AB=DE,
∴DE=DC;
(2)解:如图所示:作直径DF,连接EF.
则∠EFD=∠EAD,
∵∠CDE=∠DAE,
∴∠EFD=∠CDE.
∵DF是⊙O的直径,
∴∠DEF=90°,
∴∠EFD+∠FDE=90°,
∴∠CDE+∠FDE=90°
∴∠FDC=90°.
∴直线DC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ab2﹣2a2b+a3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.00000065mm2.这个数用科学记数法表示为( )mm2.
A. 6.5×10-6 B. 0.65×10-6 C. 65×10-6 D. 6.5×10-7
-
科目: 来源: 题型:
查看答案和解析>>【题目】铅笔每支售价0.20元,在平面直角坐标系内表示小明买1支到10支铅笔需要花费的钱数的图像是( )
A. 一条直线 B. 一条射线 C. 一条线段 D. 10个不同的点
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校对学生进行体育测试,规定参加测试的每名学生从“1.立定跳远、2.1分钟跳绳3.掷实心球、4.50米跑”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的概率是多少?
(2)据统计,初三一班共12名男生参加了“立定跳远”的测试,他们的成绩如下:
95 100 90 82 90 65 89 74 75 93 92 85
①这组数据的众数是 ,中位数是 ;
②若将不低于90分(含90分)的成绩评为优秀,请你估计初三年级选“立定跳远”的240名男生中成绩为优秀的学生约为多少人.
-
科目: 来源: 题型:
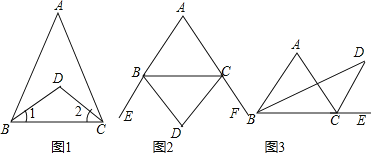
查看答案和解析>>【题目】(1)阅读并填空:如图①,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线.
试说明∠D=90°+
 ∠A的理由.
∠A的理由.解:因为BD平分∠ABC(已知),
所以∠1= (角平分线定义).
同理:∠2= .
因为∠A+∠ABC+∠ACB=180°,∠1+∠2+∠D=180°,( ),
所以∠D = (等式性质).
即:∠D=90°+
 ∠A.
∠A.(2)探究,请直接写出结果,并任选一种情况说明理由:
(i)如图②,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
(ii)如图③,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线.试探究∠D与∠A之间的等量关系.
答:∠D与∠A之间的等量关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.

相关试题

