【题目】如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
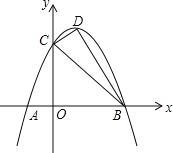
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=﹣x2+2x+3.(2)E(2,3).(3)存在,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.
【解析】
试题分析:(1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(﹣1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而可求得a=﹣1,b=2;
(2)过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点,由△BCD与△BCE是同底等高的三角形可知S△BCD=S△BCE,设直线DE的解析式为y=﹣x+b,将点D的坐标代入可求得直线DE的解析式,然后与抛物线的解析式联立可求得点E的坐标;
(3)由两点间的而距离公式可知:BC=3![]() ,CD=
,CD=![]() ,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
解:(1)∵将x=0代入得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1.
∴A(﹣1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(﹣1,0),B(3,0)代入y=ax2+bx+3得:![]() ,
,
解得:![]() .
.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵将x=1代入抛物线的解析式得:y=﹣1+2+3=4,
∴D(1,4).
如图1,过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点.
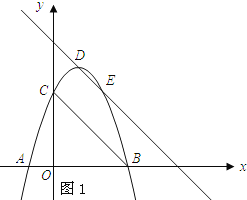
设直线DE的解析式为y=﹣x+b,
将点D的坐标代入得:﹣1+b=4,解得:b=5,则直线DE的解析式为y=﹣x+5.
将y=﹣x+5与y=﹣x2+2x+3联立得:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴E(2,3).
(3)存在.
由两点间的而距离公式可知:BC=![]() 3
3![]() ,CD=
,CD=![]() =
=![]() .
.
设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x.
①如图2所示:

∵当△BMN∽△DBC时,![]() ,
,
∴![]() .
.
解得:x1=2,x2=3(舍去).
∵当x=2时,y=3,
∴M(2,3).
②如图3所示:
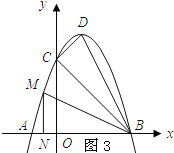
∵当△BMN∽△BDC时,![]() ,
,
∴![]() .
.
解得:x1=﹣![]() ,x2=3(舍去).
,x2=3(舍去).
当x=﹣![]() 时,y=
时,y=![]() ,
,
∴M(﹣![]() ,
,![]() )
)
综上,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,-3)在第( )象限.
A. 一
B. 二
C. 三
D. 四
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
①abc>0;②a﹣b+c>0;③2a﹣3b=0;④c﹣4b>0.你认为其中正确信息是 (填序号).
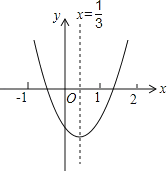
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=﹣
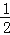 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.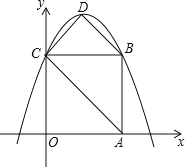
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中,不是命题的是( )
A.若两角之和为90,则这两个角互补 B.同角的余角相等
C.作线段的垂直平分线 D.相等的角是对顶角
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列描述不属于定义的是( )
A.两组对边分别平行的四边形叫做平行四边形;
B.正三角形是特殊的等腰三角形;
C.在同一平面内三条线段首尾顺次连接得到的图形叫做三角形;
D.含有未知数的等式叫做方程
-
科目: 来源: 题型:
查看答案和解析>>【题目】“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨.数据67500用科学记数法表示为( )
A. 675×102 B. 67.5×103 C. 6.75×104 D. 6.75×105
相关试题

