【题目】已知:等边三角形△ABC内接于⊙O,点D在![]() 上,连接AD、CD、BD,
上,连接AD、CD、BD,
(1)如图1,求证:∠ADB=∠BDC=60°;
(2)如图2,若BD=3CD,求证:AE=2CE;
(3)在(2)的条件下,连接OE,若BE=14,求线段OE的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.(3)![]()
【解析】
(1)根据同弧所对的圆周角相等,推出∠BDC=∠BAC=60°,∠ADC=∠ACB=60°即可解决问题.
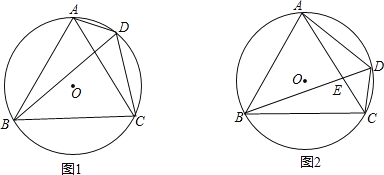
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.由△ACD≌△BCH推出BD=DA+DC,结合条件推出AD=2DC,再根据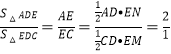 ,即可证明.
,即可证明.
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.用x表示BN、EN,在Rt△EBN中,利用勾股定理列出方程即可.
(1)证明:如图1中,
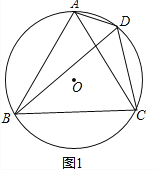
∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵∠BDC=∠BAC,∠ADC=∠ACB,
∴∠ADB=∠BDC=60°.
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.
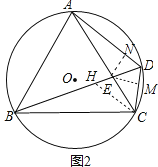
∵∠HDC=60°,DH=DC,
∴△DHC是等边三角形,
∴HC=DC,∠CHD=60°,
∴∠BCA=∠HCD=60°,
∴∠BCH=∠ACD,
在△BCH和△ACD中,
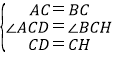 ,
,
∴△ACD≌△BCH,
∴BH=AD,
∴BD=BH+HD=AD+CD.
∵BD=3CD,
∴3CD=AD+CD,
∴AD=2CD,
∵∠ADB=∠BDC,EN⊥DA,EM⊥DC,
∴EN=EM,
∵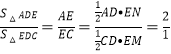 ,
,
∴AE=2CE.
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.
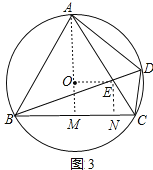
∵O是等边三角形的外心,
∴OA=2OM,∵AE=2EC,
∴![]() ,
,
∴OE∥CM,
∵AM⊥BC,
∴AO⊥OE,
∵∠OAE=![]() ∠BAC=30°,
∠BAC=30°,
∴AE=2x,EC=x,CN=![]() x,BN=
x,BN=![]() x,EN=
x,EN=![]() x
x
在Rt△BNE中,∵BE2=BN2+EN2,
∴142=(![]() x)2+(
x)2+(![]() x)2,
x)2,
∴x2=28,
∵x>0,
∴x=2![]() .
.
∴OE=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,BD,CE分别是
中,BD,CE分别是 ,
, 平分线,BD,CE相交于点P.
平分线,BD,CE相交于点P.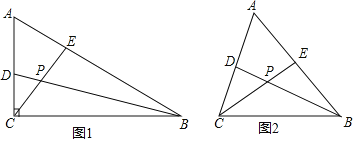
 如图1,如果
如图1,如果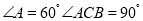 ,则
,则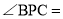 ______;
______; 如图2,如果
如图2,如果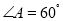 ,
,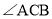 不是直角,请问在
不是直角,请问在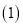 中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.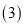 小月同学在完成
小月同学在完成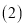 之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了
之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了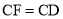 ,连接PF,可证
,连接PF,可证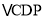 ≌
≌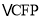 ,请你写出小月同学发现,并完成她的说理过程.
,请你写出小月同学发现,并完成她的说理过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A. 45° B. 120° C. 45°或135° D. 45°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线的解析式
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有符合条件的点P的坐标.
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=90°,AB=AC,∠B =∠ACB=45°, AE⊥AD,且AE=AD,若AB=6cm,则四边形ADCE的面积为___.

相关试题

