【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
参考答案:
【答案】(1) 每个甲种零件为200元,每个乙种零件的进价为150元;(2) 该商店本次购进甲种零件至少是16个.
【解析】(1)设每个甲种零件为x元,每个乙种零件的进价为(x-50)元,根据关键语句“用4000元购进甲种零件的数量是用l500元购进乙种零件的数量的2倍”可得方程![]() ,再解方程即可;
,再解方程即可;
(2)设购进甲种零件m个,则购进乙种零件(2m+4)个,根据题意可得不等关系:甲零件的利润+乙零件的利润≥2400元,根据不等关系列出不等式,解出解集,即可确定答案.
(1)设每个甲种零件为x元,每个乙种零件的进价为(x-50)元,由题意得:
![]() ,
,
解得:x=200,
经检验x=200是原分式方程的解,
x-50=200-50=150.
答:每个甲种零件为200元,每个乙种零件的进价为150元;
(2)设购进甲种零件m个,由题意得:
(260-200)m+(190-150)(2m+4)≥2400,
解得:m≥16.
答:该商店本次购进甲种零件至少是16个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径点F、C是半圆弧ABC上的三等份点,连接AC,AF,过点C作CD⊥AF交AF的延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知含字母m,n的代数式是:
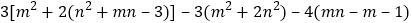 .
.(1)化简这个代数式.
(2)小明取m,n互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少?
(3)聪明的小智从化简的代数式中发现,只要字母n取一个固定的数,无论字母m取何数,代数式的值恒为一个不变的数,那么小智所取的字母n的值是多少呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
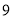

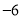
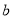
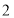
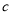
…
(1)可求得
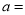 ,第
,第 个格子中的数为 ;
个格子中的数为 ;(2)若前
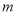 个格子中所填整数之和
个格子中所填整数之和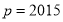 ,则
,则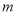 的值为多少?若
的值为多少?若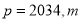 的值为多少?
的值为多少?(3)若
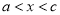 ,则
,则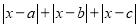 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在
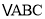 中,BD,CE分别是
中,BD,CE分别是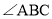 ,
,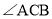 平分线,BD,CE相交于点P.
平分线,BD,CE相交于点P.
 如图1,如果
如图1,如果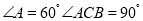 ,则
,则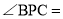 ______;
______; 如图2,如果
如图2,如果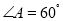 ,
,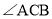 不是直角,请问在
不是直角,请问在 中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由.
中所得的结论是否仍然成立?若成立,请证明:若不成立,请说明理由. 小月同学在完成
小月同学在完成 之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了
之后,发现CD、BE、BC三者之间存在着一定的数量关系,于是她在边CB上截取了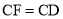 ,连接PF,可证
,连接PF,可证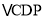 ≌
≌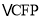 ,请你写出小月同学发现,并完成她的说理过程.
,请你写出小月同学发现,并完成她的说理过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:等边三角形△ABC内接于⊙O,点D在
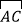 上,连接AD、CD、BD,
上,连接AD、CD、BD,(1)如图1,求证:∠ADB=∠BDC=60°;
(2)如图2,若BD=3CD,求证:AE=2CE;
(3)在(2)的条件下,连接OE,若BE=14,求线段OE的长.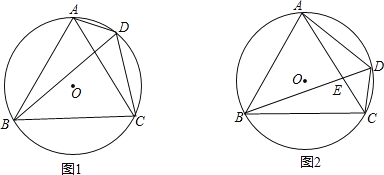
相关试题

