【题目】已知点A(-2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
参考答案:
【答案】(1)5;(2)作图见解析.
【解析】试题分析:(1)代入![]() ,以及
,以及![]() 点的坐标即可求得
点的坐标即可求得![]() 的值;
的值;
(2)根据题意求得抛物线的解析式为![]() 从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用5点式画出函数的图象即可.
从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用5点式画出函数的图象即可.
试题解析:
(1) ![]() b=1,c=3,∴y=x2+x+3.
b=1,c=3,∴y=x2+x+3.
![]() 点A(-2,n)在抛物线y=x2+bx+c上,
点A(-2,n)在抛物线y=x2+bx+c上,
![]() n=4-2+3=5.
n=4-2+3=5.
(2)解法一: ![]() A(-2,n),B(4,n)在抛物线y=x2+bx+c上,
A(-2,n),B(4,n)在抛物线y=x2+bx+c上,
![]()
![]() ∴b=-2.
∴b=-2.
![]() 顶点横坐标是-
顶点横坐标是-![]() =1,
=1,
故顶点为(1,-4).
![]() -4=1-2+c,
-4=1-2+c,
![]() c=-3,
c=-3,
![]() P(x-1,x2-2x-3).
P(x-1,x2-2x-3).
![]() 将点(x,x2-2x-3)向左平移一个单位得点P(x-1,x2-2x-3),
将点(x,x2-2x-3)向左平移一个单位得点P(x-1,x2-2x-3), ![]() 将点(x,x2-2x-3)的纵坐标随横坐标变化的函数的图象向左平移一个单位后可得点P(x-1,x2-2x-3)的纵坐标随横坐标变化的函数图象.设p=x-1,q=x2-2x-3,则q=p2-4.其函数图象如下:
将点(x,x2-2x-3)的纵坐标随横坐标变化的函数的图象向左平移一个单位后可得点P(x-1,x2-2x-3)的纵坐标随横坐标变化的函数图象.设p=x-1,q=x2-2x-3,则q=p2-4.其函数图象如下:
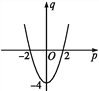
解法二:由抛物线的对称性,可知A(-2,n)与B(4,n)关于对称轴对称,则对称轴为直线x=-![]() =1,∴b=-2.
=1,∴b=-2.
又y=x2+bx+c的最小值是-4,
![]() =-4,b2-4c=16,
=-4,b2-4c=16,
![]() c=-3.
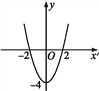
c=-3. ![]() y=x2-2x-3=(x-1)2-4,故P(x-1,x2-2x-3).令x-1=x',则P(x-1,x2-2x-3)的纵坐标随横坐标变化的函数关系式为y=x'2-4,其纵坐标随横坐标变化的图象如下:
y=x2-2x-3=(x-1)2-4,故P(x-1,x2-2x-3).令x-1=x',则P(x-1,x2-2x-3)的纵坐标随横坐标变化的函数关系式为y=x'2-4,其纵坐标随横坐标变化的图象如下:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)

-
科目: 来源: 题型:
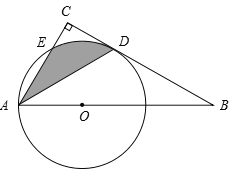
查看答案和解析>>【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC相切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π
 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频率分布表和频率直方图的一部分如下:
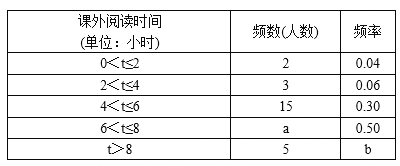

请根据图表信息回答下列问题:
(1)频数分布表中的a=____________,b=____________;
(2)将频数直方图补充完整;
(3)学校将每周课外阅读时间在6小时以上的学生评为“阅读之星”,请你估计该校2 000名学生中评为“阅读之星”的有多少人?
相关试题

