【题目】一服装批发店出售某品牌童装,每件进价120元,批发价200元,多买优惠;凡是一次买10件以上的,每多买一件,所买的全部服装每件就降低1元,但是最低价为为每件160元,
(1)求一次至少买多少件,才能以最低价购买?
(2)写出服装店一次销售x件时,获利润y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲批发了46件,乙批发了50件,店主却发现卖46件赚的钱反而比卖50件赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到多少?
参考答案:
【答案】(1)一次至少买50件,才能以最低价购买.(2)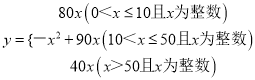 ;(3)店家应把最低价每件160元至少提高到165元.
;(3)店家应把最低价每件160元至少提高到165元.
【解析】试题分析:(1)设一次至少买x件,则每件的价格为[200-(x-10)]元,根据降价后的价格为160元建立方程求出其解即可;
(2)根据总利润=销售数量×每支的利润建立解析式即可;
(3)根据(2)的解析化为顶点式,根据顶点式的性质就可以求出结论.
试题解析:
(1)设一次至少买x件,才能以最低价购买,由题意,得
200-(x-10)×1=160,
解得:x=50.
答:一次至少买50件,才能以最低价购买.
(2)当0<x≤10时,y=(200-120)x=80x
当10<x≤50时,y=[(200-120)-(x-10)×1] ×x=-x2+90x,
当x>50时,y=(160-120)x=40x.
综上:y与x的关系式为 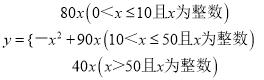
(3)由y=-x2+90x=-(x-45)2+2025 知对称轴x=45,
当45<x≤50时,y随x的增大而减小,即当卖的件数越多时,利润越小.
即出现了卖46件赚的钱比卖50件嫌的钱多的现象.
当x=45时,最低售价为200-(45-10)=165(元).
∴为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到165元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3时,整式px3+qx+1的值等于2012,那么当x=﹣3时,整式px3+qx+1的值为( )
A.2013
B.﹣2012
C.2014
D.﹣2010 -
科目: 来源: 题型:
查看答案和解析>>【题目】在某市外郊一段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,在如图所示的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在点A的北偏东45°方向上,另外一条高等级公路在y轴上,OA为其中一段.
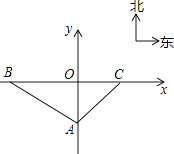
(1)求点B和C的坐标.
(2)一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该汽车在这段限速路上是否超速?(参考数据: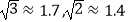 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果点A(a,b)在第三象限,则点B(-a,3b-5)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题
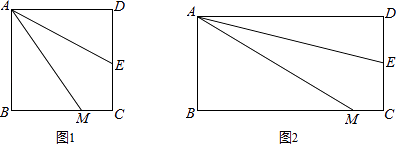
【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)【探究展示】
直接写出AM、AD、MC三条线段的数量关系:;
(2)【拓展延伸】
AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的依据是( )
A. AAS B. SAS C. HL D. SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.
相关试题

