【题目】已知函数y=2x2+4x-3.
(1)通过配方,写出抛物线的开口方向、对称轴和顶点坐标;
(2)分别求出抛物线与x轴、y轴的交点坐标.
参考答案:
【答案】(1) 对称轴是直线x=-1,顶点坐标为(-1,-5);(2) 交点坐标为(0,-3).
【解析】试题分析:(1)根据![]() 的值可直接得到二次函数的开口方向,把二次函数化成顶点式即可写出顶点坐标、对称轴;
的值可直接得到二次函数的开口方向,把二次函数化成顶点式即可写出顶点坐标、对称轴;
(2)令二次函数中![]() 求出对应的
求出对应的![]() 的值,可得到二次函数图象与
的值,可得到二次函数图象与![]() 轴的交点坐标;令二次函数中
轴的交点坐标;令二次函数中![]() 求出对应的
求出对应的![]() 的值,可得到二次函数图象与
的值,可得到二次函数图象与![]() 轴的交点坐标;
轴的交点坐标;
试题解析:
(1)y=2x2+4x-3=2(x2+2x)-3=2(x2+2x+1-1)-3=2(x+1)2-5.
![]() 抛物线开口向上,对称轴是直线x=-1,顶点坐标为(-1,-5).
抛物线开口向上,对称轴是直线x=-1,顶点坐标为(-1,-5).
(2)令y=0,得2x2+4x-3=0,解得x1=![]() ,x2=-
,x2=-![]() .
.
![]() 抛物线与x轴的交点坐标为
抛物线与x轴的交点坐标为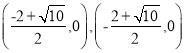 .
.
令x=0,得y=-3.
![]() 抛物线与y轴的交点坐标为(0,-3).
抛物线与y轴的交点坐标为(0,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 hcm,则 h 的取值范围是( )
A.h≤15cmB.h≥8cmC.8cm≤h≤17cmD.7cm≤h≤16cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
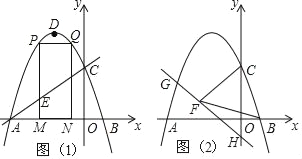
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一个横断面为抛物线形状的拱桥,当水面宽4 m时,拱顶(拱桥洞的最高点)离水面2 m,当水面下降1 m时,水面的宽度为_____m.

-
科目: 来源: 题型:
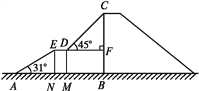
查看答案和解析>>【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形的对角线分别为 x、y,一边长为 12,则 x、y 的值可能是( )
A.8 与 14B.10 与 14C.18 与 20D.4 与 28
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
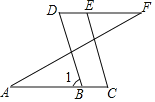
解:∵∠A=∠F(已知)
∴AC∥DF(______)
∴∠D=∠1(______)
又∵∠C=∠D(已知)
∴∠1=______
∴BD∥CE(______)
相关试题

