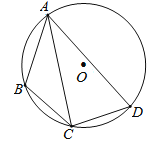
【题目】如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是 .
参考答案:
【答案】![]() .
.
【解析】
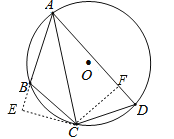
试题分析:过C作CE⊥AB于E,CF⊥AD于F,则∠E=∠CFD=∠CFA=90°,∵点C为弧BD的中点,∴![]() ,∴∠BAC=∠DAC,BC=CD,∵CE⊥AB,CF⊥AD,∴CE=CF,∵A、B、C、D四点共圆,∴∠D=∠CBE,在△CBE和△CDF中,∵∠CBE=∠D,∠E=∠CFD,CE=CF,∴△CBE≌△CDF,∴BE=DF,在△AEC和△AFC中,∵∠E=∠AFC,∠EAC=∠FAC,AC=AC,∴△AEC≌△AFC,∴AE=AF,设BE=DF=x,∵AB=3,AD=5,∴AE=AF=x+3,∴5=x+3+x,解得:x=1,即AE=4,∴AC=
,∴∠BAC=∠DAC,BC=CD,∵CE⊥AB,CF⊥AD,∴CE=CF,∵A、B、C、D四点共圆,∴∠D=∠CBE,在△CBE和△CDF中,∵∠CBE=∠D,∠E=∠CFD,CE=CF,∴△CBE≌△CDF,∴BE=DF,在△AEC和△AFC中,∵∠E=∠AFC,∠EAC=∠FAC,AC=AC,∴△AEC≌△AFC,∴AE=AF,设BE=DF=x,∵AB=3,AD=5,∴AE=AF=x+3,∴5=x+3+x,解得:x=1,即AE=4,∴AC=![]() =
=![]() ,故答案为:
,故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)5 (2
(2 )+(3
)+(3 )(+4
)(+4 )
)
(2) (
(
 +
+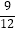 )×(24)
)×(24)
(3)(3)÷ ×
× ×(15)
×(15)
(4)-14+|(-2)3-10|-(-3)÷(-1)2017 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关圆的一些结论,其中正确的是( )
A.任意三点可以确定一个圆B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦,并且平分弦所对的弧D.圆内接四边形对角互补
-
科目: 来源: 题型:
查看答案和解析>>【题目】请在你的班里做一项有关师生关系的调查,分四个方面:①自由平等的师生关系②既注重师道尊严,又注重平等的师生关系③传统的尊师爱生的关系④不太协调的关系,请你统计出四个方面的人数,回答以下问题.
①列出表格,并作出相应的统计图.
②任取一名同学,他与老师之间的关系是自由平等的师生关系,是哪一种事件?可能性约为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算a2a4的结果是( )
A.a8
B.a6
C.2a6
D.2a8 -
科目: 来源: 题型:
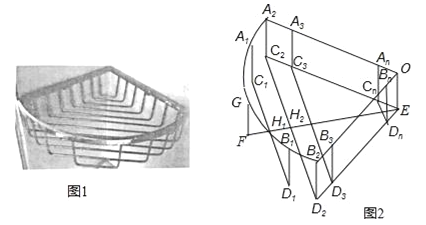
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
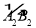 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=
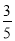 ,CQ=5,求AF的值.
,CQ=5,求AF的值.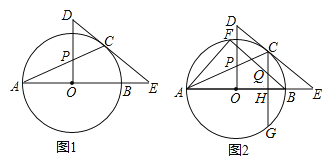
相关试题

