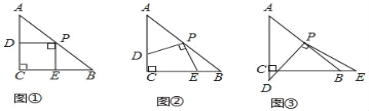
【题目】如图,在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:
(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?结合图②说明理由.
(2)三角板绕点P旋转,△PCE是否能成为等腰三角形?若能,指出所有情况(直接写答案).
参考答案:
【答案】(1)PD=PE,证明见解析;(2)△PCE能成为等腰三角形,证明见解析
【解析】
(1)PD=PE,通过证△DPC≌△EPB,可得结论
(2)分三种情况讨论①当PC=PE=![]() 时;②当PC=CE=
时;②当PC=CE=![]() 时;③当PE=EC时,可求解.
时;③当PE=EC时,可求解.
解:(1)PD=PE,理由如下:
当D在AC上时,连接PC,

因为△ABC是等腰直角三角形,P是AB的中点,
∴CP=PB,CP⊥AB,∠ACP=![]() ∠ACB=45°.
∠ACB=45°.
∴∠ACP=∠B=45°.
又∵∠DPC+∠CPE=∠BPE+∠CPE,
∴∠DPC=∠BPE.
∴△PCD≌△PBE.
∴PD=PE;
当D在AC上时,连接PC,

因为△ABC是等腰直角三角形,P是AB的中点,
∴CP=PB,CP⊥AB,∠ACP=![]() ∠ACB=45°.
∠ACB=45°.
∴∠ACP=∠CBP=45°.
∴∠PCD=∠PBE=135°.
又∵∠DPC+∠DPB=∠DPB+∠BPE,
∴∠DPC=∠BPE.
∴△PCD≌△PBE.
∴PD=PE
综上所述:PD=PE;
(2)△PBE是等腰三角形,理由如下:
∵AC=BC=2,∠C=90°
∴AB=2![]()
∴AP=BP=CP=![]()
△PCE是等腰三角形
当PC=PE=![]() 时,即B,E重合,BE=0
时,即B,E重合,BE=0
当PC=CE=![]() 时,且E在线段BC上,则BE=2﹣
时,且E在线段BC上,则BE=2﹣![]()
当PC=CE=![]() 时,且E在线段BC的延长线上,则BE=2+
时,且E在线段BC的延长线上,则BE=2+![]()
当PE=EC,且∠PCB=45°
∴∠PEC=90°
∴EC=1
∴BE=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=
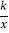 (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是∠AOB的角平分线OC上的任意一点.
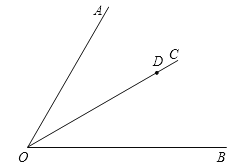
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OC,垂足为点D,DF与OB交于点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于_____mm(精确到1mm);
(2)在(1)所画出的图形中,若∠AOB=n,则∠EDF=____________度(用含n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)
(k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)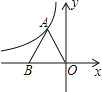
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△ABC向上平移多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列解答中,填写适当的理由或数学式:
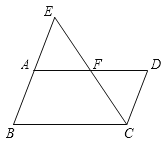
(1)∵EB∥DC, (已知)
∴∠DAE=∠__. ( ___________________________________)
(2)∵∠BCF+∠AFC=180°,(已知)
∴ ____∥___. ( ___________________________________)
(3)∵ ____∥___, (已知)
∴∠EFA=∠ECB . ( ___________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有九张背面一模一样的扑克牌,正面分别为:红桃A、红桃2、红桃3、红桃4、黑桃A、黑桃2、黑桃3、黑桃4、黑桃5.
(1)现将这九张扑克牌混合均匀后背面朝上放置,若从中摸出一张,求正面写有数字3的概率是多少?
(2)现将这九张扑克牌分成红桃和黑桃两部分后背面朝上放置,并将红桃正面数字记作m,黑桃正面数字记作n,若从黑桃和红桃中各任意摸一张,求关于x的方程mx2+3x+
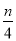 =0有实根的概率.(用列表法或画树形图法解,A代表数字1)
=0有实根的概率.(用列表法或画树形图法解,A代表数字1)
相关试题

