【题目】如图,点D是∠AOB的角平分线OC上的任意一点.
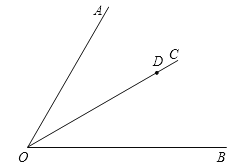
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OC,垂足为点D,DF与OB交于点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于_____mm(精确到1mm);
(2)在(1)所画出的图形中,若∠AOB=n,则∠EDF=____________度(用含n的代数式表示).
参考答案:
【答案】(1)①详见解析;②详见解析;③20;(2)(90-![]() n)
n)
【解析】
(1)根据题中要求作出相应平行线和垂线,然后量出DG的长度;
(2)根据角平分线可得∠AOD=∠COB=![]() °,又因为平行可得∠ODE=∠AOD=
°,又因为平行可得∠ODE=∠AOD=![]() °,即可得到∠EDF=(90-
°,即可得到∠EDF=(90-![]() n)°
n)°
解:(1)①②③如图1所示;
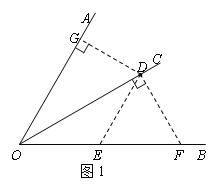
③ 20(允许误差范围20±3);
(2)∵OC平分∠AOB
∴∠AOD=∠COB=![]() °
°
又∵OA∥DE
∴∠ODE=∠AOD=![]() °
°
∵DF⊥OC
∴∠ODF=90°
∴∠EDF=(90-![]() n)°
n)°
故答案为 (90-![]() n) .
n) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
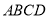 ,
,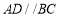 ,点
,点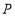 在直线
在直线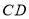 上运动(点
上运动(点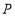 和点
和点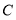 ,
, 不重合,点
不重合,点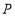 ,
,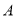 ,
,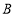 不在同一条直线上),若记
不在同一条直线上),若记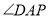 ,
,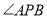 ,
,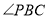 分别为
分别为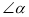 ,
, ,
,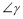 .
.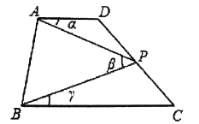
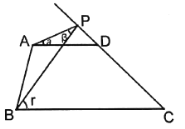
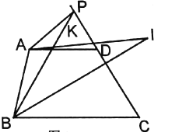
图1 图2 图3
(1)如图1,当点
 在线段
在线段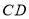 上运动时,写出
上运动时,写出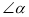 ,
, ,
,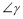 之间的关系,并说出理由;
之间的关系,并说出理由;(2)如图2,如果点
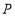 在线段
在线段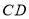 的延长线上运动,探究
的延长线上运动,探究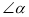 ,
, ,
,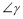 之间的关系,并说明理由.
之间的关系,并说明理由.(3)如图3,
 平分
平分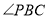 ,
,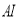 交
交 于点
于点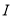 ,交
,交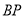 于点
于点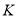 ,且
,且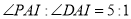 ,
,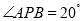 ,
,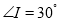 ,求
,求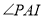 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车制造厂开发了一款新式自行车,计划
 月份生产安装
月份生产安装 辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现:
辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人;他们经过培训后也能独立进行安装.调研部门发现:  名熟练工和
名熟练工和 名新工人每日可安装辆自行车;
名新工人每日可安装辆自行车;  名熟练工和
名熟练工和 名新工人每日可安装
名新工人每日可安装 辆自行车。
辆自行车。(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘
 名新工人(
名新工人( ).使得招聘的新工人和抽调熟练工刚好能完成
).使得招聘的新工人和抽调熟练工刚好能完成 月份(
月份( 天)的安装任务,那么工厂有哪几种新工人的招聘方案?
天)的安装任务,那么工厂有哪几种新工人的招聘方案?(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为
 千公里;如安装在后轮,安全行使路程为
千公里;如安装在后轮,安全行使路程为 千公里.请问一对轮胎能行使的最长路程是多少千公里?
千公里.请问一对轮胎能行使的最长路程是多少千公里? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=
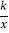 (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
-
科目: 来源: 题型:
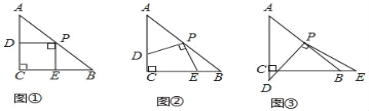
查看答案和解析>>【题目】如图,在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①、②、③是旋转三角板得到的图形中的3种情况,研究:
(1)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?结合图②说明理由.
(2)三角板绕点P旋转,△PCE是否能成为等腰三角形?若能,指出所有情况(直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)
(k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)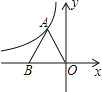
(1)求反比例函数的表达式;
(2)若要使点B在上述反比例函数的图象上,需将△ABC向上平移多少个单位长度?
相关试题

