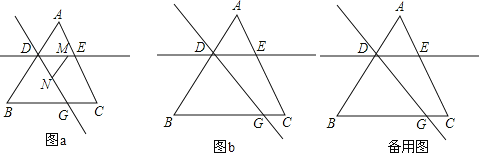
【题目】三角形ABC中,G是BC上一点,D,E分别在边AB,AC上,DE∥BC,M为直线DE上一点,N为直线GD上一点,∠DMN=∠B
(1)如图a,当点M在DE上,点N在DG上时,求证:∠BDN=∠MND;
(2)当点M在ED延长线上,点N在GD延长线上时,请在图b中画出图形,此时∠BDN与∠MND的数量关系是 _________ ;
(3)在(2)的条件下,延长DG交AC延长线于点F,若∠A=60°,∠MND=75°,求∠F的度数.
参考答案:
【答案】(1)证明见解析;(2)∠BDN+∠MND=180°;(3)15°.
【解析】分析:(1)利用平行线的性质得出∠B=∠ADE,进而得出AB∥MN,即可得出答案;(2)利用(1)中解题思路,首先判断AB∥MN,进而利用平行线的性质得出;(3)利用(2)所求得出∠MND=∠ADN=75°,进而利用三角形的外角得出即可.
本题解析:
(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN=∠MND;
(2)解:如图(b),∵DE∥BC,
∴∠B=∠ADE,
∵∠DMN=∠B,
∴∠ADE=∠DMN,
∴AB∥MN,
∴∠BDN+∠MND=180°,
故答案为:∠BDN+∠MND=180°;
(3)解:如备用图,由(2)得:AB∥MN,
∴∠MND=∠ADN=75°,
∵∠A+∠F=∠ADN=75°,∠A=60°,
∴∠F=15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简﹣2(m﹣n)的结果为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x﹣y=3,m+n=2,则(x+m)﹣(y﹣n)的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣4xay+x2yb=﹣3x2y,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个外角都是45°,则这个多边形的边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1)。按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣2,3)]等于( )
A. (﹣2,﹣3) B. (2,﹣3) C. (﹣2,3) D. (2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积.
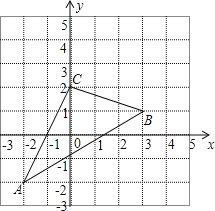
相关试题

