【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC. 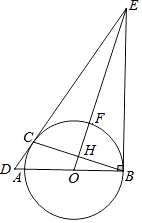
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB= ![]() ,求AC的长.
,求AC的长. 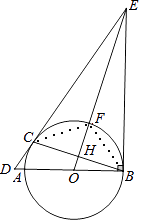
参考答案:
【答案】
(1)解:证明:∵BE⊥OB,
∴BE是⊙O的切线,∵EC是⊙O的切线,
∴EC=EB,
∴∠ECB=∠EBC
(2)解:连接CF、CO、AC.
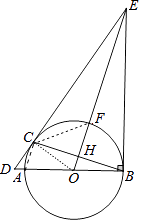
∵EB=EC,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,
在Rt△CFH中,∵CF=6,sin∠FCH= ![]() ,
,
∴FH=CFsin∠FCH= ![]() ,CH=
,CH= ![]() =
= ![]() ,
,
设OC=OF=x,
在Rt△COH中,∵OC2=CH2+OH2,
∴x2=( ![]() )2+(x﹣
)2+(x﹣ ![]() )2,
)2,
∴x=5,
∴OH= ![]() ,
,
∵OH⊥BC,
∴CH=HB,∵OA=OB,
∴AC=2OH= ![]() .
.
【解析】(1)只要证明EB是⊙O的切线,利用切线长定理可知EC=EB,即可解决问题.(2)连接CF、CO、AC.在Rt△CFH中,由CF=6,sin∠FCH= ![]() ,推出FH=CFsin∠FCH=
,推出FH=CFsin∠FCH= ![]() ,CH=
,CH= ![]() =
= ![]() ,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2 , 可得x2=(
,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2 , 可得x2=( ![]() )2+(x﹣
)2+(x﹣ ![]() )2 , 解得x=5,推出OH=
)2 , 解得x=5,推出OH= ![]() ,再利用三角形中位线定理证明AC=2OH即可解决问题.
,再利用三角形中位线定理证明AC=2OH即可解决问题.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图2,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )

A. ① B. ② C. ①② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形 ABCD 的面积为 16,△ABE 是等边三角形,点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为_____________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC 和等边△BPE,点 P 在 BC 的延长线上,EC 的延长线交 AP 于点 M,连接 BM;下列结论:①AP=CE;②∠PME=60°;③BM 平分∠AME;④AM+MC=BM,其中正确的有____________________(填序号).
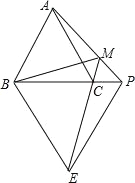
-
科目: 来源: 题型:
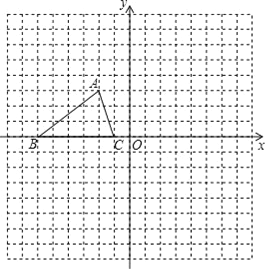
查看答案和解析>>【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0).
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是______.
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是______.
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为______.
-
科目: 来源: 题型:
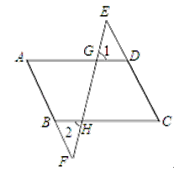
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
-
科目: 来源: 题型:
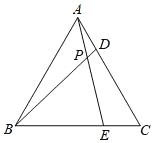
查看答案和解析>>【题目】如图,△ABC 为等边三角形,D、E 分别是边 AC、BC 上的点,且AD=CE,AE 与 BD 相交于点 P.
(1)求∠BPE 的度数;
(2)若 BF⊥AE 于点 F,试判断 BP 与 PF 的数量关系并说明理由.
相关试题

