搜索
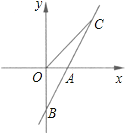
【题目】如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
（1）求直线AB的解析式；
（2）若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．
参考答案：
【答案】（1）直线AB的解析式为y=2x﹣2；（2）点C的坐标是（2，2）.
【解析】试题分析：（1）设直线
的解析式为
将点
点
分别代入解析式即可组成方程组，从而得到
的解析式；
（2）设点
的坐标为
根据三角形面积公式以及
求出
的横坐标，再代入直线即可求出
的值，从而得到其坐标．
试题解析：(1)设直线AB的解析式为y=kx+b(k≠0).
∵直线AB过点A(1,0)、点B(0,2)，
解得
∴直线AB的解析式为y=2x2.
(2)设点C的坐标为(x,y)，
∵
解得x=2，
∵直线AB的解析式为y=2x2，
∴当x=2时，y=2×22=2，
∴点C的坐标是(2,2).
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：﹣12÷（﹣3）= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a＞b，若c是任意实数，则下列不等式中总成立的是（ ）
A.a+c＜b+cB.a﹣c＞b﹣cC.ac＜bcD.ac＞bc
-
科目： 来源： 题型：
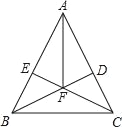
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
【答案】证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边)，
在△ABF和△ACF中，
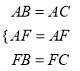，∴△ABF≌△ACF(SSS)，
∴∠BAF=∠CAF(全等三角形对应角相等)，
∴AF平分∠BAC.
【题型】解答题
【结束】
23【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．
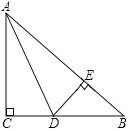
（1）求证：CD=BE；
（2）已知CD=2，求AC的长；
（3）求证：AB=AC+CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式计算正确的是（ ）
A.（x+y）2＝x2+y2B.（x+3）（x﹣3）＝x2﹣3
C.（m﹣n）（n﹣m）＝n2﹣m2D.（x﹣y）2＝（y﹣x）2
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种生物细胞的直径约为0.00056米，用科学记数法表示为____________米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一篇文章中，“的”、“地”、“和”三个字共出现50次，已知“的”和“地”出现的频率之和是0.7，那么“和”字出现的频数是（ ）
A. 14 B. 15 C. 16 D. 17
相关试题
