【题目】某旅行杜拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?
参考答案:
【答案】(1)超过200人;(2)甲学校报名参加旅游的学生有160人,乙学校报名参加旅游的学生有80人.
【解析】
(1)由已知分两种情况讨论,即a>200,和100<a≤200,得出结论;
(2)根据两种情况的费用,即x>200,和100<x≤200,分别设未知数列方程求解,讨论得到答案.
(1)设两校人数之和为a,
若a>200,则a=18000÷75=240,
若100<a≤200,则a=18000÷85=211![]() >200,不符合题意,
>200,不符合题意,
故两所学校报名参加旅游的学生人数之和等于240人,故超过200人;
(2)设甲学校报名参加旅游的学生有x人,
则①100<x≤200时,
85x+90(240-x)=20800
解得x=160
240-x=80,
②当x>200时,
75x+90(240-x)=20800
解得x=53![]() (不符题意,舍去)
(不符题意,舍去)
故甲学校报名参加旅游的学生有160人,乙学校报名参加旅游的学生有80人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小强上山游玩,小颖乘坐缆车,小强步行,两人相约在山顶的缆车终点会和,已知小强行走到缆车终点的路程是缆车到山顶的线路长的
 倍,小颖在小强出发后
倍,小颖在小强出发后 分才乘上缆车,缆车的平均速度为
分才乘上缆车,缆车的平均速度为 米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.
米/分,若图中的折线表示小强在整个行走过程中的路程(米)与出发时间(分)之间的关系的图像,请回答下列问题.
(1)小强行走的总路程是 米,他途中休息了 分;
(2)分别求出小强在休息前和休息后所走的两段路程的速度;
(3)当小颖到达缆车终点时,小强离缆车终点的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
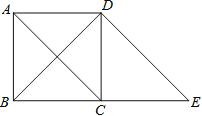
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知小正方形 ABCD 的面积为1,把它的各边延长一倍得到新正方形 A 1 B 1 C 1 D 1 ;把正方形 A 1 B 1 C 1 D 1 边长按原法延长一倍得到正方形 A 2 B 2 C 2 D 2 (如图(2));以此下去,则正方形 A n B n C n D n 的面积为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一副秋千架,左图是从正面看,当秋千绳子自然下垂时,踏板离地面0.5m(踏板厚度忽略不计), 右图是从侧面看,当秋千踏板荡起至点B位置时,点B离地面垂直高度BC为1m,离秋千支柱AD的水平距离BE为1.5m(不考虑支柱的直径).求秋千支柱AD的高.


-
科目: 来源: 题型:
查看答案和解析>>【题目】用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )
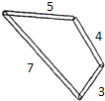
A.6B.7C.8D.9
相关试题

