Question

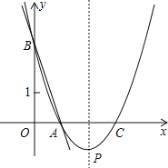
【题目】如图，直线y=-3x+3与x轴、y轴分别交于点A、B，抛物线经过点A、B，并与x轴交于另一点C，其顶点为P．

（1）求，的值；

（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；

（3）在抛物线及其对称轴上分别取点M、N，使以A，C，M，N为顶点的四边形为正方形，求此正方形的边长．

Answer 1

【答案】（1）a，k的值分别为1，﹣1；（2）（2，2）；（3）

【解析】

试题分析：（1）先求出直线y=-3x+3与x轴交点A，与y轴交点B的坐标，再将A、B两点坐标代入y=a（x-2）2+k，得到关于a，k的二元一次方程组，解方程组即可求解；

（2）设Q点的坐标为（2，m），对称轴x=2交x轴于点F，过点B作BE垂直于直线x=2于点E．在Rt△AQF与Rt△BQE中，用勾股定理分别表示出AQ2=AF2+QF2=1+m2，BQ2=BE2+EQ2=4+（3-m）2，由AQ=BQ，得到方程1+m2=4+（3-m）2，解方程求出m=2，即可求得Q点的坐标；

（3）当点N在对称轴上时，由NC与AC不垂直，得出AC为正方形的对角线，根据抛物线的对称性及正方形的性质，得到M点与顶点P（2，-1）重合，N点为点P关于x轴的对称点，此时，MF=NF=AF=CF=1，且AC⊥MN，则四边形AMCN为正方形，在Rt△AFN中根据勾股定理即可求出正方形的边长．

试题解析：（1）∵直线y=﹣3x+3与x轴、y轴分别交于点A、B，

∴A（1，0），B（0，3）．

又∵抛物线抛物线y=a（x﹣2）2+k经过点A（1，0），B（0，3），

∴， 解得，

故a，k的值分别为1，﹣1；

（2）如图，设Q点的坐标为（2，m），对称轴x=2交x轴于点F，

过点B作BE垂直于直线x=2于点E．

在Rt△AQF中，AQ2=AF2+QF2=1+m2，

在Rt△BQE中，BQ2=BE2+EQ2=4+（3﹣m）2，

∵AQ=BQ，∴1+m2=4+（3﹣m）2，

∴m=2，

∴Q点的坐标为（2，2）；

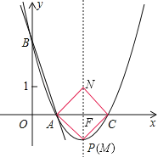
（3）当点N在对称轴上时，NC与AC不垂直，所以AC应为正方形的对角线．

又∵对称轴x=2是AC的垂直平分线，M为抛物线上的点.

∴M点与顶点P（2，﹣1）重合，N点为点P关于x轴的对称点，

其坐标为N（2，1）．

此时，MF=NF=AF=CF=1，且AC⊥MN， ∴四边形AMCN为正方形．

在Rt△AFN中，AN==，即正方形的边长为．