【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
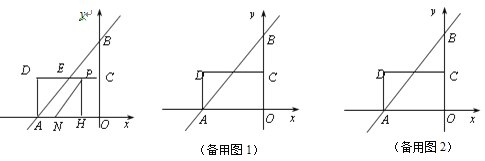
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为t秒.
,垂足为H,连接NP.设点P的运动时间为t秒.
① 若△NPH的面积为1,求t的值;
② 点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
参考答案:
【答案】(1)、A(-3,0)、B(0,4);E(-![]() ,2);(2)、①、t=1或2;②、P(-2,2)
,2);(2)、①、t=1或2;②、P(-2,2)
【解析】
试题分析:(1)、根据一次函数得出A、B两点的坐标,根据矩形的性质得出点E的坐标;(2)、设PC=t,AN=t,NO=3-t,首先求出t的取值范围,得到NH=3jain2t,然后利用面积求出t的值;根据题意得出点Q的坐标,作QQ′平行且等于PH,易证四边形QQ/PH为平行四边形,得到点Q′的坐标,然后设出直线BQ′的解析式,把点Q′的坐标代入求出k的值,然后得出点P的坐标.
试题解析:(1)、A(-3,0),B(0,4) ∵C(0,2) ∴0C=2 ∵四边形ABCD是矩形 ∴AO∥CD
∴当y=2时,x=-![]() ∴E(-
∴E(-![]() ,2)
,2)
(2)、①PC=t,AN=t,NO=3-t, 3-t>t ∴t<![]()
当0<t<![]() 时,NH=3-t-t=3-2t ∴S=
时,NH=3-t-t=3-2t ∴S=![]() ×2×(3-2t)=1 解得:t=1
×2×(3-2t)=1 解得:t=1
3-t<t,∴t>![]() 当
当![]() <t≤3 NH=2t-3 ∴S=
<t≤3 NH=2t-3 ∴S=![]() ×2×(2t-3)=1 解得:t=2
×2×(2t-3)=1 解得:t=2
所以t=1或t=2
②易得Q(-6,-4),作QQ′平行且等于PH,易证四边形QQ/PH为平行四边形, Q′(-6,-2)
设BQ′直线的解析式为y=kx+4(k≠0) 把Q′(-6,-2)代入得到k=1
当y=2时x=-2,此时t=2 故存在P(-2,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2不具有的性质是( )
A.开口向上
B.对称轴是y轴
C.在对称轴的左侧,y随x的增大而增大
D.最高点是原点 -
科目: 来源: 题型:
查看答案和解析>>【题目】在|﹣2|,﹣|0|,(﹣2)5,﹣|﹣2|,+(﹣2)中,负数共有( )
A. 1 个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )
A.y1<y2<y3
B.y1<y3<y2
C.y3<y2<y1
D.y2<y1<y3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=5,AB=3,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适合全面调查方式的是( )
A. 调查全国人民的环保意识 B. 调查中秋节期间市场月饼的质量
C. 调查某班40名同学的体重 D. 调查某类烟花爆炸燃放安全质量
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我校八年级同学的视力情况,从八年级的15个班共590名学生中,每班随机抽取了5名进行分析。在这个问题中.样本是____________________,样本容量是______.
相关试题

