【题目】(1)已知![]() =4,且(y- 2z+1)2+
=4,且(y- 2z+1)2+![]() =0,求
=0,求![]() 的值;
的值;
(2)若关于x,y的二元一次方程组![]() 的解满足x+y>-
的解满足x+y>- ![]() ,求出满足条件的m的所有正整数值.
,求出满足条件的m的所有正整数值.
参考答案:
【答案】 (1) 6;(2) 1,2,3.
【解析】试题分析:(1)依据立方根的性质可求得x的值,然后利用非负数的性质可求得y,z的值,然后代入计算即可;
(2)因为方程组中x的系数为2和1,y的系数为 1和2,和都为3,所以将两式相加即可使得x、y的系数都为3,进而可以把x+y用m表示,然后代入x+y>![]() 求出m的范围,即可得出m的正整数值.
求出m的范围,即可得出m的正整数值.
试题解析:
解:(1)∵![]() =4,∴x=43=64,
=4,∴x=43=64,
又∵(y- 2z+1)2+![]() =0,
=0,
∴y- 2z+1=0且z- 3=0,
解得z=3,y=5.
∴![]() =6;
=6;
(2) ![]()
①+②得3(x+y)=-3m+6,
∴x+y=-m+2,
∵x+y>- ![]() ,
,
∴-m+2>-![]() ,
,
∴m<![]() ,
,
∵m为正整数,
∴m可取1,2,3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌对第一季度A、B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图10所示:
(1)一月份B款运动鞋的销售量是A款的
 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?(2)第一季度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议。

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣6x+5=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七边形的内角和为( )
A.540°B.720°C.900°D.1080°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:86,85,82,97,73这组数据的中位数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题:“如果|a|=|b|,那么a=b”的逆命题是:____(填“真命题”或“假命题”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
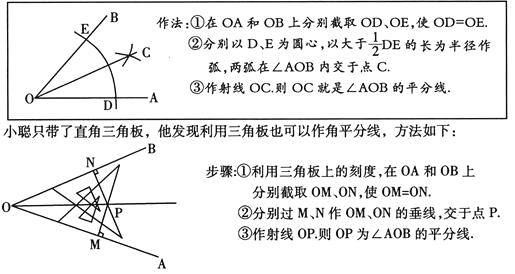
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
相关试题

