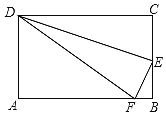
【题目】如图所示,沿DE折叠长方形ABCD的一边,使点C落在AB边上的点F处,若AD=8,且△AFD的面积为60,则△DEC的面积为( )
A. ![]()
B. ![]()
C. 18
D. 20
参考答案:
【答案】A
【解析】
由矩形的性质得出∠A=∠B=90°,BC=AD=8,CD=AB,结合△AFD的面积为60,即可求得AF与DF的长,由折叠的性质,可得CD=DF,然后在Rt△BEF中,利用勾股定理即可求得CE的长,继而求得△DEC的面积.
∵四边形ABCD是矩形,
∴∠A=∠B=90°,BC=AD=8,CD=AB,
∵△AFD的面积为60,
即![]() ADAF=60,
ADAF=60,
解得:AF=15,
∴DF=![]() =
=![]() =17,
=17,
由折叠的性质,得:CD=DF=17,
∴AB=17,
∴BF=AB-AF=17-15=2,
设CE=x,则EF=CE=x,BE=BC-CE=8-x,
在Rt△BEF中,EF2=BF2+BE2,
即x2=22+(8-x)2,
解得:x=![]() ,
,
即CE=![]() ,
,
∴△DEC的面积=![]() CDCE=
CDCE=![]() ×17×
×17×![]() =
=![]() ;
;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-
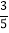 [(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.(1)求m,n的值;
(2)点N为抛物线上的一动点,且位于直线BC上方,连接CN,BN.求△NBC面积的最大值.
-
科目: 来源: 题型:
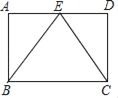
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是边AD的中点,连接BE、CE.
(1)求证:△ABE≌△DCE;
(2)当BC=2AB,求∠BEC的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
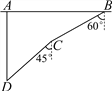
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
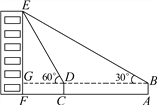
-
科目: 来源: 题型:
查看答案和解析>>【题目】李晖到“宇泉牌”服装专卖店做社会调查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员
小俐
小花
月销售件数(件)
200
150
月总收入(元)
1400
1250
假设月销售件数为
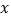 件,月总收入为
件,月总收入为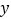 元,销售每件奖励
元,销售每件奖励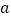 元,营业员月基本工资为
元,营业员月基本工资为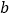 元.
元.(1)求
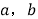 的值;
的值;(2)若营业员小俐某月总收入不低于
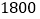 元,那么小俐当月至少要卖服装多少件?
元,那么小俐当月至少要卖服装多少件?
相关试题

