搜索
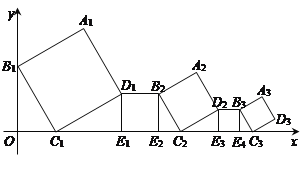
【题目】一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1，E1，E2，C2，E3，E4，C3……在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O＝60°，B1C1∥B2C2∥B3C3……则正方形A2017B2017C2017D2017的边长是____；
参考答案：
【答案】
【解析】利用正方形的性质结合锐角三角函数关系得出正方形的边长，进而得出变化规律即可得出答案.
解：易知△B2C2E2∽△C1D1E1，∴
＝
＝
＝
30°．
∴B2C2＝C1D1·30°＝
．∴C2D2＝．
同理，B3C3＝C2D2·30°＝()2；
由此猜想BnCn＝()n－1．
当n＝2017时，B2017C2017＝()2016．
“点睛”此题主要考查了正方形的性质以及锐角三角函数等知识，得出正方形的边长变化规律是解题的关键.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一条东西走向的商业街上，依次有书店（记为A）、冷饮店（记为B）、鞋店（记为C），冷饮店位于鞋店西边50m处，鞋店位于书店东边60m处，王平先去书店，然后沿着这条街向东走了30m至D处，接着向西走50m到达E处．
（1）以A为原点、向东为正方向画数轴，在数轴上表示出上述A，B，C，D，E的位置；
（2）若在这条街上建一家超市，使超市与鞋店C分居E点两侧，且到E点的距离相等，问超市在冷饮店的什么方向？距离多远？
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着社会的发展，通过微信朋友圈发布自己每天行走的步数已经成为一种时尚．“健身达人”小陈为了了解他的好友的运动情况．随机抽取了部分好友进行调查，把他们6月1日那天行走的情况分为四个类别：A（0～5000步）（说明：“0～5000”表示大于等于0，小于等于5000，下同），B（5001～10000步），C（10001～15000步），D（15000步以上），统计结果如图所示：
请依据统计结果回答下列问题：
（1）本次调查中，一共调查了 位好友．
（2）已知A类好友人数是D类好友人数的5倍．
①请补全条形图；
②扇形图中，“A”对应扇形的圆心角为 度．
③若小陈微信朋友圈共有好友150人，请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步？
-
科目： 来源： 题型：
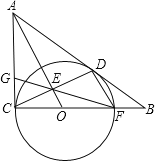
查看答案和解析>>【题目】如图，⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D，与边BC相交于点F，OA与CD相交于点E，连接FE并延长交AC边于点G．
（1）求证：DF∥AO；
（2）若AC=6，AB=10，求CG的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填在相应的括号内
， -
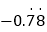, 0,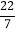 
,‐3.1415926, 20%, ‐3
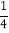, 2, -1，3.1010010001…（每两个1之间逐次增加1个0） ①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形
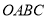中， 
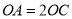，顶点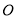
在坐标原点，顶点
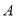的坐标为(8,6).(1)顶点
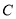的坐标为( ， )，顶点
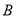的坐标为( ， );(2)现有动点
、
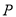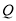分别从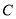
、
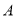同时出发，点
沿线段
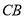向终点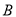
运动，速度为每秒2个单位，点
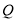沿折线
→
→
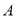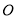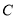向终点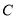
运动，速度为每秒
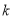个单位.当运动时间为2秒时，以点
、
、
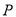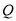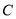顶点的三角形是等腰三角形，求
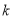的值.(3)若矩形
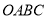以每秒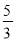
个单位的速度沿射线
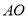下滑，直至顶点
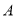到达坐标原点时停止下滑.设矩形
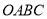在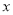
轴下方部分的面积为
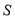，求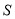
关于滑行时间
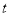的函数关系式，并写出相应自变量
的取值范围.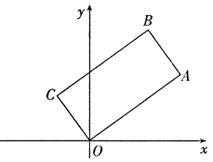
-
科目： 来源： 题型：
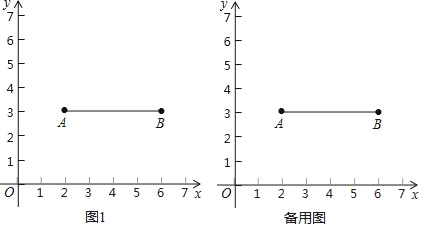
查看答案和解析>>【题目】如图，在平面直角坐标系中，给出如下定义：已知点A（2，3），点B（6，3），连接AB．如果线段AB上有一个点与点P的距离不大于1，那么称点P是线段AB的“环绕点”．
（1）已知点C（3，1.5），D（4，3.5），E（1，3），则是线段AB的“环绕点”的点是 ；
（2）已知点P（m，n）在反比例函数y=
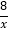的图象上，且点P是线段AB的“环绕点”，求出点P的横坐标m的取值范围；（3）已知⊙M上有一点P是线段AB的“环绕点”，且点M（4，1），求⊙M的半径r的取值范围．
相关试题
