【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图:
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H .
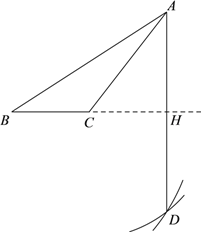
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是___________.他的依据是_____________________.
参考答案:
【答案】 小明;到线段两个端点距离相等的点在线段的垂直平分线上(答案不唯一); 两点确定一条直线(答案不唯一).
【解析】根据已知条件可知直线BC是线段AD的垂直平分线,由此一一判定即可.
解:(1)小明;到线段两个端点距离相等的点在线段的垂直平分线上(答案不唯一);
如图连接CD、BD,
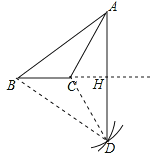
∵CA=CD,BA=BD,
∴点C、点B在线段AD的垂直平分线上,
∴直线BC是线段AD的垂直平分线.
“点睛”本题考查作图-基本作图、线段的垂直平分线的性质等知识,解题的关键是掌握证明线段垂直平分线的证明方法,属于基础题,中考常考题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年10月12日至15日,第二届中国“互联网+”大学生创新创业全国总决赛上,ofo共享单车从全国约119000个创业项目中脱颖而出,最终获得金奖. 将119000用科学计数法表示应为
A.
 B.
B.  C.
C.  D.
D. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线l上顺次取A,B,C三点,使得AB=4cm,BC=3cm,如果O为线段AC的中点,M为线段AB的中点,N为线段BC的中点.
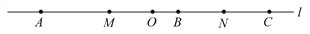
(1)求线段MN的长度;
(2)求线段OB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子摆出下列一组图形.
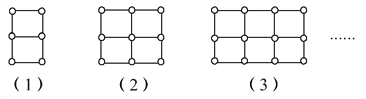
(1)填写下表:

(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;
(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
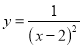 的图象与性质,小静根据学习函数的经验,对函数
的图象与性质,小静根据学习函数的经验,对函数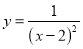 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整:(1)函数
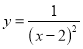 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;(2)下表是y与x的几组对应值.
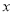
…
-1
0
1

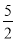
3
4
…

…
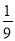

1
4
m
1
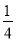
…
表中的m=__________;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;

(4)结合函数图象,写出一条该函数图象的性质:______________________________.
相关试题

