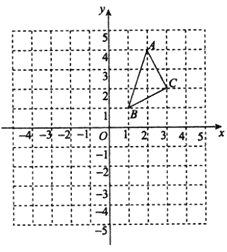
【题目】△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
(1)作出△ABC关于x轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点A2、B2、C2的坐标.
参考答案:
【答案】(1)作图见解析,A1(2,-4),B1(1,-1),C1(3,-2).(2)作图见解析,A2(-2,-4),B2(-1,-1),C2(-3,-2).
【解析】
(1)分别作出各点关于x轴的对称点,再顺次连接,再写出点A1、B1、C1的坐标即可;
(2)△A2B2C2的坐标与△ABC的关系是,横坐标互为相反数,纵坐标互为相反数;找到点画出即可.
(1)如图,△A1B1C1,即为所求,由图可知,A1(2,-4),B1(1,-1),C1(3,-2).
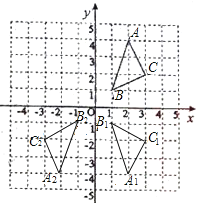
(2)如图所示,A2(-2,-4),B2(-1,-1),C2(-3,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】南果梨是东北辽宁省的一大特产,现有20筐南国梨,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值
(单位:千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐南果梨中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐南果梨总计超过或不足多少千克?
(3)若南果梨每千克售价4元,则这20筐可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=﹣2x+1,下列结论正确的是( )
A. 图象必经过点(﹣2,1) B. 图象经过第一、二、三象限
C. 当x>
 时,y<0 D. y随x的增大而增大
时,y<0 D. y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:①13+(﹣22)﹣(﹣2)
②﹣4
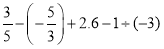
③(
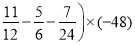 ×(﹣48)
×(﹣48)④﹣14﹣(
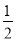 ﹣1)[﹣23+(﹣3)2]
﹣1)[﹣23+(﹣3)2](2)化简:①(3mn﹣2m2)+(﹣4m2﹣5mn)
②﹣(2a﹣3b)﹣2(﹣a+4b﹣1)
(3)先化简再求值:7x2y﹣2(2x2y﹣3xy2)-(4x2y﹣xy2),其中x=﹣2,y=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学从家到学校的距离之比是10:7,甲同学的家与学校的距离为3000米,甲同学乘公交车去学校、乙同学骑自行车去学校.已知公交车速度是乙骑自行车速度的2倍,甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙同学的家与学校的距离为多少米?
(2)求乙骑自行车的速度.
相关试题

