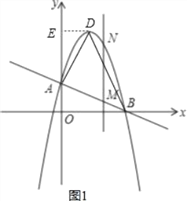
【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=![]() ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?

参考答案:
【答案】(1)y=﹣![]() x+2;(2)
x+2;(2)![]() (3)当t=2时,MN的长度l有最大值,最大值是4.
(3)当t=2时,MN的长度l有最大值,最大值是4.
【解析】(1)∵在Rt△AOB中,tan∠ABO=![]() ,OA=2,即
,OA=2,即![]() =
=![]() ,
,
∴0B=4,∴A(0,2),B(4,0),
把A、B的坐标代入y=﹣x2+bx+c得: ![]() ,解得:b=
,解得:b=![]() ,
,
∴抛物线的解析式为y=﹣x2+![]() x+2,
x+2,
设直线AB的解析式为y=kx+e,把A、B的坐标代入得: ![]() ,
,
解得:k=﹣![]() ,e=2,
,e=2,
所以直线AB的解析式是y=﹣![]() x+2;
x+2;
(2)过点D作DE⊥y轴于点E,
由(1)抛物线解析式为y=﹣x2+![]() x+2=﹣(x﹣
x+2=﹣(x﹣![]() )2+
)2+![]() ,
,
即D的坐标为(![]() ,
, ![]() ),则ED=
),则ED=![]() ,EO=
,EO=![]() ,AE=EO﹣OA=
,AE=EO﹣OA=![]() ,
,
S△ABD=S梯形DEOB﹣S△DEA﹣S△AOB=![]() ×(
×(![]() +4)×
+4)×![]() ﹣
﹣![]() ×
×![]() ×
×![]() ﹣
﹣![]() ×4×2=
×4×2=![]() ;
;
(3)由题可知,M、N横坐标均为t.
∵M在直线AB:y=﹣![]() x+2上,∴M(t,﹣
x+2上,∴M(t,﹣![]() t+2),
t+2),
∵N在抛物线y=﹣x2+![]() x+2上,∴M(t,﹣t2+
x+2上,∴M(t,﹣t2+![]() t+2),
t+2),
∵作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N,
∴MN=﹣t2+![]() t+2﹣(﹣
t+2﹣(﹣![]() +2)=﹣t2+4t=﹣(t﹣2)2+4,其中0<t<4,
+2)=﹣t2+4t=﹣(t﹣2)2+4,其中0<t<4,
∴当t=2时,MN最大=4,
所以当t=2时,MN的长度l有最大值,最大值是4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中, AB=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒.
(1)如图1,S△DCP = .(用t的代数式表示)
(2)如图1,当t=3时,试说明:△ABP≌△DCP.
(3)如图2,当点P从点B开始运动的同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
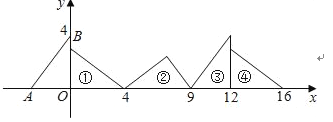

A. (60,0) B. (72,0) C. (67
 ,
, ) D. (79
) D. (79 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在RtABC中,∠C=90°,AC=BC=
 (如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.
(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面程序计算,即根据输入的
 判断
判断 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的 的值作为新的
的值作为新的 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有 的值是__.
的值是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

相关试题

