【题目】如图,一次函数![]() =
=![]() 的图像与正比例函数
的图像与正比例函数![]() =
=![]() 的图像相交于点A(2,
的图像相交于点A(2,![]() ),与
),与![]() 轴相交于点B.
轴相交于点B.

(1)求![]() 、
、![]() 的值;
的值;
(2)在![]() 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
参考答案:
【答案】(1)a=1,b=2;(2)点C的坐标为(0,2)或(0,-2).
【解析】
(1)利用正比例函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标,利用待定系数法即可求出b的值;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,根据三角形的面积公式结合△AOC的面积等于△AOB的面积,即可得出点C的坐标.
解:(1)把点A(2,a)的坐标代入y=![]() x,解得a=1.
x,解得a=1.
把点A(2,1)的坐标代入y=-![]() x+b,解得b=2.
x+b,解得b=2.
(2)把y=0代入y=-![]() x+2,解得x=4.
x+2,解得x=4.
∴点B的坐标为(4,0).
∴OB=4.
∵S△AOC=S△AOB,
∴![]() ×2·OC=
×2·OC=![]() ×4×1.
×4×1.
∴OC=2.
∴点C的坐标为(0,2)或(0,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=
 (k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA= 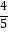 .
.
(1)求边AB的长;
(2)求反比例函数的解析式和m的值;
(3)若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一点
 从数轴上表示
从数轴上表示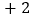 的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……(1)写出第一次移动后这个点在数轴上表示的数;
(2)写出第
 次移动后这个点在数轴上表示的数;
次移动后这个点在数轴上表示的数;(3)如果第
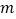 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求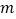 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.
(1)求BC的长;
(2)如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.
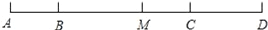
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:时间(第x天)
1
3
6
10
…
日销售量(m件)
198
194
188
180
…
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天)
1≤x<50
50≤x≤90
销售价格(元/件)
x+60
100
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
相关试题

