【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动. 
(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
参考答案:
【答案】
(1)解:设点M、N运动x秒后,M、N两点重合,
x×1+12=2x,
解得:x=12
(2)解:设点M、N运动t秒后,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=12﹣2t,
∵三角形△AMN是等边三角形,
∴t=12﹣2t,
解得t=4,
∴点M、N运动4秒后,可得到等边三角形△AMN

(3)解:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∵  ,
,
∴△ACM≌△ABN,
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,CM=NB,
y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.

【解析】(1)首先设点M、N运动x秒后,M、N两点重合,表示出M,N的运动路程,N的运动路程比M的运动路程多12cm,列出方程求解即可;(2)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN三角形ANM就是等边三角形;(3)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若整式x2+ky2(k为不等于零的常数)能在有理数范围内因式分解,则k的值可以是(写出一个即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:18°36′=__°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮和小明沿同一条路同时从学校出发到市图书馆,学校与图书馆的路程是4千米,小亮骑自行车,小明步行,当小亮从原路回到学校时,小明刚好到达市图书馆,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分)之间的函数关系,根据图象提供信息,下列结论错误的是( )

A. 小亮在图书馆停留的时间是15分钟
B. 小亮从学校去图书馆的速度和从图书馆返回学校的速度相同
C. 小明离开学校的路程s(千米)与时间t(分)之间的函数关系式为S=

D. BC段s(千米)与t(分)之间的函数关系式为S=
 +12
+12 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加速内蒙古经济建设,国家计划投资204.4亿元修建赤峰市至喀左的“高铁”,204.4亿用科学记数法表示正确的是( )
A.0.2044×1011
B.20.44×109
C.2.044×108
D.2.044×1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠CAB=90°,AC=AB=6,D,E分别是AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;
(2)如图2,当α=135°时,设直线BD1与CA的交点为F,求证:BD1=CE1,且BD1⊥CE1;
(3)点P到AB所在直线的距离的最大值是 .

-
科目: 来源: 题型:
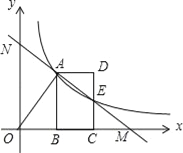
查看答案和解析>>【题目】如图,O为原点,反比例函数y=
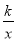 (x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).(1)反比例函数的解析式为 ;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=
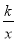 (x>0)的图象恰好经过DC的中点E,
(x>0)的图象恰好经过DC的中点E,①求直线AE的函数表达式;
②若直线AE与x轴交于点M,与y轴交于点N,请你写出线段AN与线段ME的大小,并说明理由.
相关试题

