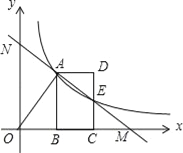
【题目】如图,O为原点,反比例函数y=![]() (x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
(1)反比例函数的解析式为 ;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=![]() (x>0)的图象恰好经过DC的中点E,
(x>0)的图象恰好经过DC的中点E,
①求直线AE的函数表达式;
②若直线AE与x轴交于点M,与y轴交于点N,请你写出线段AN与线段ME的大小,并说明理由.
参考答案:
【答案】(1)反比例函数的解析式为![]() ;
;
(2)①直线AE的函数表达式为y=mx+n;
②线段AN=ME,理由见解析.
【解析】试题分析:(1)把A点的坐标解析式即可求出k的值;(2)①根据点E是CD的中点,得出点E的坐标,即可求出直线AE的解析式;②求出直线AE与坐标轴的交点坐标,利用平行线分线段成比例定理得出结论即可.
试题解析:(1)∵点A(2,3)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=2×3=6,
∴反比例函数的解析式为y=![]() (x>0).
(x>0).
故答案为:y=![]() (x>0).
(x>0).
(2)∵AB=CD,点E为线段CD的中点,
∴点E的纵坐标为![]() ,
,
将y=![]() 代入y=
代入y=![]() 中,则有
中,则有![]() =
=![]() ,
,
解得:x=4,
∴点E的坐标为(4,![]() ).
).
设直线AE的表达式为y=mx+n,
将点A(2,3)、E(4,![]() )代入y=mx+n中得:
)代入y=mx+n中得: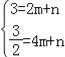 ,
,
解得: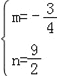 ,
,
∴直线AE的表达式为y=﹣![]() x+
x+![]() .
.
(3)AN=ME,利用如下:
令y=﹣![]() x+
x+![]() 中y=0,则0=﹣
中y=0,则0=﹣![]() x+
x+![]() ,
,
解得:x=6,
∴点M的坐标为(6,0).
∵点A(2,3)、E(4,![]() ),
),
∴点B(2,0),点C(4,0),
∴点B、C为线段OM的三等分点,
∵AB∥CD(平移的性质),
∴点A、E为线段MN的三等分点,
∴AN=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了加速内蒙古经济建设,国家计划投资204.4亿元修建赤峰市至喀左的“高铁”,204.4亿用科学记数法表示正确的是( )
A.0.2044×1011
B.20.44×109
C.2.044×108
D.2.044×1010 -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠CAB=90°,AC=AB=6,D,E分别是AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;
(2)如图2,当α=135°时,设直线BD1与CA的交点为F,求证:BD1=CE1,且BD1⊥CE1;
(3)点P到AB所在直线的距离的最大值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:a是不为1的有理数,我们把
 称为a的差倒数,如2的差倒数是
称为a的差倒数,如2的差倒数是  =﹣1,﹣1的差倒数是
=﹣1,﹣1的差倒数是  =
=  .已知a1=﹣
.已知a1=﹣  ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,求a2016的值.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,求a2016的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣2x2﹣4x+1,先用配方法转化成y=a(x﹣h)2+k,再写出函数的顶点坐标、对称轴以及描述该函数的增减性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户2014年承包荒山若干亩,改造后,种果树2000棵,总投资7800元,2015年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用含a、b表示两种方式出售水果的收入;
(2)若a=1.3,b=1.1,且两种出售水果方式都在相同时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
相关试题

