【题目】小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计)一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校公用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的个数是( )
A.4个
B.3个
C.2个
D.1个
参考答案:
【答案】B
【解析】解:∵小刚从家出发7分钟时与家的距离是1200米,即小刚从家出发7分钟时距离学校3500﹣1200=2300m,
∴公交车的速度为: ![]() =400米/分钟,故①正确;
=400米/分钟,故①正确;
由①知公交车速度为400米/分钟,
∴公交车行驶的时间为 ![]() =7分钟,
=7分钟,
∴小刚从家出发乘上公交车是在第12﹣7=5分钟时,故②正确;
∵从上公交车到他到达学校公用10分钟,
∴小刚下公交车后跑向学校的速度是 ![]() =100米/分钟,故③正确;
=100米/分钟,故③正确;
∵小刚从下车至到达学校所用时间为5+10﹣12=3分钟,
而小刚下车时发现还有4分钟上课,
∴小刚下车较上课提前1分钟,故④错误;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E,K分别在边BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG; ②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
(4)当
 =
= 时,请直接写出
时,请直接写出 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
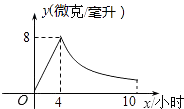
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.

(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与C,B两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形.
②设△BCF的面积为S,求S与m的函数关系式;当m为何值时,S有最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)如图,△ABC中,∠ACB=90°,D.E分别是BC、BA的中点,联结DE,F在DE延长线上,且AF=AE.
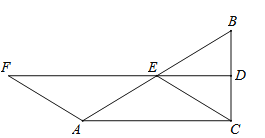
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )

A.
B.
C.2
D.
-
科目: 来源: 题型:
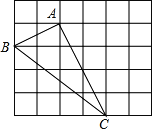
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解决下列问题:
(1)通过计算判断△ABC的形状;
(2)在图中确定一个格点D,连接AD、CD,使四边形ABCD为平行四边形,并求出 □ABCD的面积.
相关试题

