【题目】如图,矩形ABCD的边BC与x轴重合,连接对角线BD交y轴于点E,过点A作AG⊥BD于点G,直线GF交AD于点F,AB、OC的长分别是一元二次方程x-5x+6=0的两根(AB>OC),且tan∠ADB=![]() .
.
(1)求点E、点G的坐标;
(2)直线GF分△AGD为△AGF与△DGF两个三角形,且S△AGF:S△DGF =3:1,求直线GF的解析式;
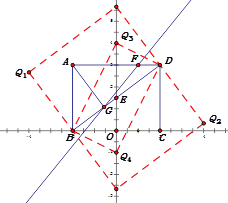
(3)点P在y轴上,在坐标平面内是否存在一点Q,使以点B、D、P、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
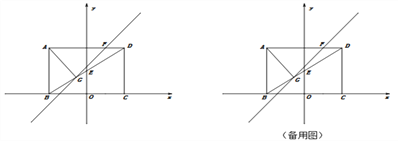
参考答案:
【答案】(1)E(0, ![]() ),G(
),G(![]() ,
, ![]() );(2)
);(2)![]() ;(3)存在Q1(-4,
;(3)存在Q1(-4, ![]() );Q2(4,
);Q2(4, ![]() );Q3(0,4);Q4(0,-1).
);Q3(0,4);Q4(0,-1).
【解析】(1)根据一元二次方程x-5x+6=0的解、tan∠ADB=![]() ,可求出点E的坐标;由△BGH∽△BDC,利用相似三角形的性质可求出点G的坐标;
,可求出点E的坐标;由△BGH∽△BDC,利用相似三角形的性质可求出点G的坐标;
(2)根据G、F的坐标,利用待定系数法可求出直线GF的解析式;
(3)对BD是矩形的边还是矩形的对角线进行分类讨论即可.
解:(1)x-5x+6=0,解得x1=2;x2=3
∵AB>OC,
∴AB=3;OC=2
∵tan∠ADB=![]() ,
,
∴AD=BC=4;BD=5
∴OE=![]() ,∴E(0,
,∴E(0, ![]() )
)
∵AG⊥BD,则△ABG∽△ABD,
![]() ,即
,即![]() ,BG=
,BG=![]() ,
,
做GH⊥x轴,由△BGH∽△BDC,

∴G(![]() ,
, ![]() )
)
(2)∵S△AGF:S△DGF =3:1,
∴AF:DF=3:1,
∴DF=1 F(1,3)
设直线GF: ![]() ,
,
代入G(![]() ,
, ![]() ),F(1,3)
),F(1,3)
∴直线GF![]()
(3)存在Q1(-4, ![]() );Q2(4,
);Q2(4, ![]() );Q3(0,4);Q4(0,-1)
);Q3(0,4);Q4(0,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】科学家研究发现,声音在空气中传播的速度y(米/秒)与气温x(°C)有关,当气温是0°C时,音速是331米/秒;当气温是5°C时,音速是334米/秒;当气温是10°C时,音速是337米/秒;气温是15°C时,音速是340米/秒;气温是20℃时,音速是343米/秒;气温是25°C时,音速是346米/秒;气温是30°C时,音速是349米/秒.
(1)请你用表格表示气温与音速之间的关系;
(2)表格反映了哪两个变量之间的关系?哪个是自变量?哪一个是对应的值?
(3)当气温是35°C时,估计音速y可能是多少?
(4)能否用一个式子来表示两个变量之间的关系?
-
科目: 来源: 题型:
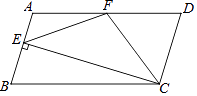
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB于E,在线段 AB上,连接EF、CF.则下列结论:①∠BCD=2∠DCF;②∠ECF=∠CEF;③S△BEC=2S△CEF;④∠DFE=3∠AEF,其中一定正确的是( )
A.②④
B.①②④
C.①②③④
D.②③④ -
科目: 来源: 题型:
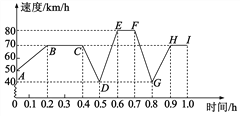
查看答案和解析>>【题目】汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快乐,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.
(1)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(2)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?
(3)用自己的语言大致描述这辆汽车的行驶情况,包括遇到的山路,在山路上的速度变化情况等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中运算错误的是( )
A.5x﹣2x=3x
B.5ab﹣5ba=0
C.4x2y﹣5xy2=﹣x2y
D.3x2+2x2=5x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】现有如下4个命题:①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
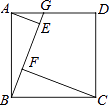
查看答案和解析>>【题目】如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2= .
相关试题

