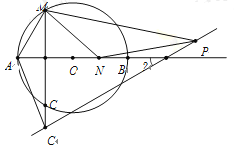
【题目】如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
(1)若AM=AC,点N与点O重合,则α= °;
(2)若点C、点N的位置如图所示,求α的度数;
(3)当直线PC与⊙O相切时,则MC的长为 .
参考答案:
【答案】(1)30(2)30°(3)![]()
【解析】
试题分析:(1)根据AM=AC,MC垂直平分AO,OM=OA,可求得△MAO的形状,然后根据点C在圆上,AP是圆O的直径,从而可以求得α的值;
(2)根据AM=AC,MC垂直平分AO,OM=OA,可求得△MAO的形状,△MNP∽△MAC,从而可以求得∠AMC和α的值;
(3)根据题意和图形,以及(2)中的α的值,直线PC与圆O相切,可以分别求得MD、DC的长,从而可以求得MC的长.
试题解析:(1)如图 ,α= 30 °;
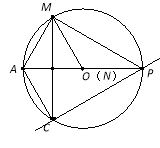
如图一所示:
∵AM=AC,MC垂直平分AO,OM=OA
∴MA=AC=MO=OA
∵点M在圆上
∴点C在圆上
∵AP是圆O的直径
∴∠ACP=90°
∵AP=2AC
∴∠APC=30°
即α=30°
(2)连接MO,

∵MC垂直平分AO,∴MA=MO=AO
∴∠AMO=60°,则∠AMC=30°
∵△MAQ∽△MNP,
∴![]() ,
,![]() ,
,
∴∠AMN=∠QMP,
∴△AMN∽△QMP,
∴∠MAN=∠MQP,
∴α=∠AMQ=30°;
(3)连接OE,如图三所示
∵AB=2,MC垂直平分AO
∴AO=1,DO=![]() ,MD=
,MD=![]()
由(2)可得α=30°
∵OE=1,∠OEF=90°
∴OF=2OE=2
∴DF=![]()
∴DC=DF·tanα=![]()
∴MC=MD+DC=![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标为( )
A. (3,3) B. (3,-3) C. (6,-6) D. (3,3)或(6,-6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数的百位数字为5,十位数字为a,个位数字为b,则
(1)这个三位数是__;
(2)把个位数字和百位数字交换位置,所得的三位数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
①甲种作物受环境影响最小;②乙种作物平均成活率最高;
③丙种作物最适合播种在山腰;
④如果每种作物只能在一个地方播种,那么山脚,山腰和山顶分别播种甲,乙,丙三种作物能使得成活率最高.其中合理的是( )

A. ①③ B. ①④ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

-
科目: 来源: 题型:
查看答案和解析>>【题目】电视机厂生产电视,八月份计划生产6 400台,已经生产了25天,再生产20台,就完成计划,这25天平均每天生产多少台根据题意,设这25天平均每天生产x台,那么方程为 _____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
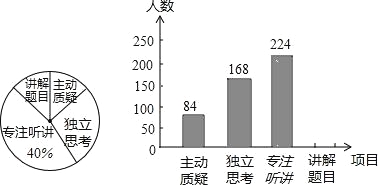
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
相关试题

