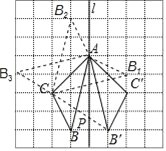
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

参考答案:
【答案】(1)画图见解析;(2)S△ABC=3;(3)作图见解析;(4)作图见解析.
【解析】(1)分别作各点关于直线l的对称点,再顺次连接即可;(2)利用矩形的面积减去三个顶点上三角形的面积即可;(3)根据勾股定理找出图形即可;(4)连接B′C交直线l于点P,则P点即为所求.
解:(1)如图,△AB′C′即为所求;
(2)S△ABC=2×4﹣![]() ×2×1﹣
×2×1﹣![]() ×1×4﹣
×1×4﹣![]() ×2×2=8﹣1﹣2﹣2=3.
×2×2=8﹣1﹣2﹣2=3.
故答案为:3;
(3)如图,△AB1C,△AB2C,△AB3C即为所求.
故答案为:3;
(4)如图,P点即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上用22根火柴棒首尾相接围成等腰三角形,这样的等腰三角形一共可以围成_________种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年12月13日,嫦娥二号成功飞抵距地球约700万公里远的深空,7 000 000用科学记数法表示为( )
A.7×105
B.7×106
C.70×106
D.7×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线与x轴交于A(6,0)、B(
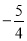 ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.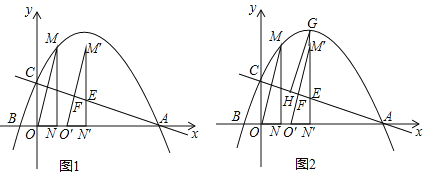
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中有红球4个,白球若干个,它们只有颜色上的区别.从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )
A.3个
B.不足3个
C.4个
D.5个或5个以上 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣11﹣8﹣(﹣3)
(2)﹣22+(﹣3)×[(﹣4)2+2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.
(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
相关试题

