【题目】
(1)计算:|﹣ ![]() |+2﹣1+
|+2﹣1+ ![]() (π﹣
(π﹣ ![]() )0﹣tan60°;
)0﹣tan60°;
(2)解分式方程: ![]() .
.
参考答案:
【答案】
(1)
解:原式= ![]() +
+ ![]() +
+ ![]() ×1﹣
×1﹣ ![]() =1
=1
(2)
解:方程的两边同乘(x+1)(x﹣1),得
2(x﹣1)+4=x2﹣1,
即x2﹣2x﹣3=0,
(x﹣3)(x+1)=0,
解得x1=3,x2=﹣1,
检验:把x=3代入(x﹣1)(x+1)=8≠0,即x=3是原分式方程的解,
把x=﹣1代入(x+1)(x﹣1)=0,即x=﹣1不是原分式方程的解,
则原方程的解为:x=3.
【解析】(1)由绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,即可将原式化简为 ![]() +
+ ![]() +
+ ![]() ×1﹣
×1﹣ ![]() ,继而求得答案;(2)观察可得最简公分母是(x+1)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
,继而求得答案;(2)观察可得最简公分母是(x+1)(x﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.
-
科目: 来源: 题型:
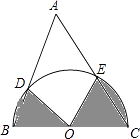
查看答案和解析>>【题目】如图,在△ABC中,∠A=50°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中阴影部分面积之和等于(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作AC⊥MN于点C,过B作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA+PB的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7
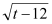 (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为
 的大正方形,两块是边长都为
的大正方形,两块是边长都为 的小正方形,五块是长为
的小正方形,五块是长为 、宽为
、宽为 的全等小矩形,且
的全等小矩形,且 >
>  .(以上长度单位:cm)
.(以上长度单位:cm)(1)观察图形,可以发现代数式
 可以因式分解为 ;
可以因式分解为 ;(2)若每块小矩形的面积为10
 ,四个正方形的面积和为58
,四个正方形的面积和为58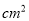 ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.
相关试题

