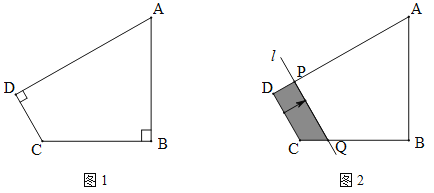
【题目】(2016四川省乐山市第23题)如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=![]() .
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q (点Q运动到点B停止),设DP=x,四边形PQCD的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出自变量
的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() ).
).
【解析】
试题分析:(1)分别延长AD、BC相交于点E,在Rt△ABE中,解直角三角形可得BE,EC,AE的长,又∠E+∠A=90°,∠E+∠ECD=90°,得到∠A=∠ECD,由tanA=![]() ,得到cosA= cos∠ECD =
,得到cosA= cos∠ECD =![]() ,从而得到CD的长;
,从而得到CD的长;
(2)由(1)可知tan∠ECD=![]() ,得到ED=
,得到ED=![]() ,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=
,由PQ∥DC,可知△EDC∽△EPQ,得到PQ=![]() ,由
,由![]() ,得到y=
,得到y=![]() ,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=
,而当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,得到DM=ED=![]() ,故可得自变量x的取值范围.
,故可得自变量x的取值范围.
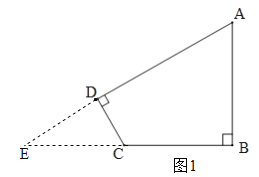
试题解析:(1)如图1,分别延长AD、BC相交于点E,在Rt△ABE中,∵tanA=![]() ,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=
,AB=3,BC=2,∴BE=4,EC=2,AE=5,又∠E+∠A=90°,∠E+∠ECD=90°,∴∠A=∠ECD,∵tanA=![]() ,∴cosA=
,∴cosA=![]() ,∴cos∠ECD=
,∴cos∠ECD=![]() ,∴CD=
,∴CD=![]() ;
;
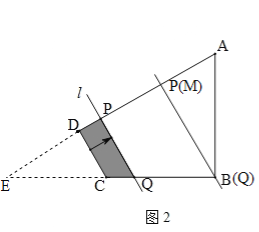
(2)由(1)可知tan∠ECD=![]() ,∴ED=
,∴ED=![]() ,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴
,如图2,由PQ∥DC,可知△EDC∽△EPQ,∴![]() ,∴
,∴ ,即PQ=
,即PQ=![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() =
=![]() ,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=
,∴当Q点到达B点时,点P在M点处,由EC=BC,DC∥PQ,∴DM=ED=![]() ,∴自变量x的取值范围为:
,∴自变量x的取值范围为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1纳米=0.000 000 001米,则2.5纳米应表示为( )米.
A.2.5×10﹣8
B.2.5×10﹣9
C.2.5×10﹣10
D.2.5×109 -
科目: 来源: 题型:
查看答案和解析>>【题目】五箱梨的质量(单位:kg)分别为:18,20,21,18,19,则这五箱梨质量的中位数和众数分别为( )
A.20和18
B.20和19
C.18和18
D.19和18 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司第4月份投入1000万元科研经费,计划6月份投入科研经费比4月多500万元.设该公司第5、6个月投放科研经费的月平均增长率为x,则所列方程正确的为( )
A. 1000(1+x)2=1000+500
B. 1000(1+x)2=500
C. 500(1+x)2=1000
D. 1000(1+2x)=1000+500
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长为15cm,其中一边长为7 cm,则底边长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程ax2+(a-3)x-3=0有两个实数根,则a的取值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个二次函数解析式,使它的图象的顶点在y轴上:_____.
相关试题

