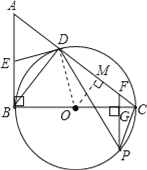
【题目】如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(1)求证:ED是⊙O的切线;
(2)求证:△CFP∽△CPD;
(3)如果CF=1,CP=2,sinA=![]() ,求O到DC的距离.
,求O到DC的距离.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)O到DC的距离为![]() .
.
【解析】试题分析:(1)连接OD,证OD⊥DE即可.易证∠ADB=90°,又点E为AB的中点,得DE=EB.根据等腰三角形性质可证∠ODE=∠OBE=90°,得证;
(2)可证∠A=∠DBC,所以要求BC需先求DC.结合已知条件,证明△PDC与△FPC相似.
(3)根据△PCF∽△DCP,得出CD的长度,进而求出O到DC的距离即可.
试题解析:(1)连接OD.
∵BC为直径,
∴△BDC为直角三角形.
在Rt△ADB中,E为AB中点,
∴BE=DE,
∴∠EBD=∠EDB.
又∵OB=OD,∴∠OBD=∠ODB,
∵∠OBD+∠ABD=90°,∴∠ODB+∠EDB=90°.
∴ED是⊙O的切线.
(2)∵PF⊥BC,
∴∠FPC=90°﹣∠BCP(直角三角形的两个锐角互余).
∵∠PDC=90°﹣∠PDB(直径所对的圆周角是直角),∠PDB=∠BCP(同弧所对的圆周角相等),
∴∠FPC=∠PDC(等量代换).
又∵∠PCF是公共角,
∴△PCF∽△DCP.
(3)过点O作OM⊥CD于点M,
∵△PCF∽△DCP,
∴PC2=CFCD(相似三角形的对应边成比例).
∵CF=1,CP=2,
∴CD=4.
可知sin∠DBC=sinA=sin∠MOC=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴直径BC=5,
∴![]() =
=![]() ,
,
∴MC=2,
∴MO=![]() ,
,
∴O到DC的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人
面试
笔试
形体
口才
专业水平
创新能力
甲
86
90
96
92
乙
92
88
95
93
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人购进一批苹果到市场上零售,已知卖出苹果数量x与售价y的关系如下表.
数量x(千克)
1
2
3
4
5
售价y(元)
3+0.1
6+0.2
9+0.3
12+0.4
15+0.5
则当卖出苹果数量为10千克时,售价y为_______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式x2﹣4x+m分解因式的结果为(x+a)(x﹣6),求2a﹣m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y轴上的点P到原点的距离为5,则点P的坐标为( )
A.(5,0)
B.(0,5)或(0,﹣5)
C.(0,5)
D.(5,0)或(﹣5,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(x-1)2=x2-2x-1B.(a-b)2=a2-b2
C.(a+m)(b+n)=ab+mnD.(m+n)(-m+n)=n2-m2
-
科目: 来源: 题型:
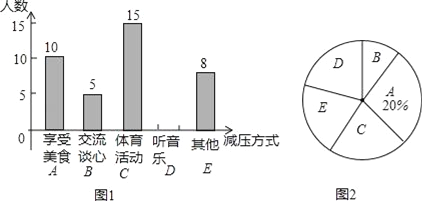
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
相关试题

