【题目】已知:如图①、②,解答下面各题:
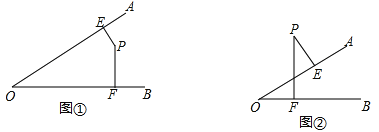
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数。
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)
参考答案:
【答案】(1)125°;(2)∠P=∠O;(3)相等或互补;(4)相等或互补.
【解析】试题分析:(1)利用四边形的内角和定理即可求解;
(2)利用垂直的定义和三角形的内角和定理求解;
(3)根据(1)和(2)的结果即可求解;
(4)本题应分两种情况讨论,如图,∠1,∠2,∠3的两边互相平行,由图形可以看出∠1和∠2是邻补角,它们和∠3的关系容易知道一个相等,一个互补.
试题解析:(1)如图①,
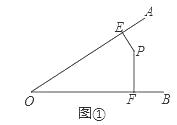
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
∴∠EPF=360°-90°-90°-55°=125°;
(2)如图②,
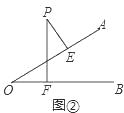
∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
又∵∠OGF=∠PGE,
∴∠P=∠O;
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补;
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角相等或互补.
如图③,
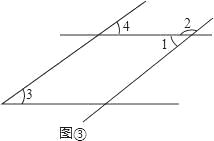
∠1,∠2,∠3的两边互相平行,
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠1,∠3+∠2=180°.
∴这两个角相等或互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个外角都等于36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2,﹣2,3,﹣3这四个数中,最小的数是( )
A. 2 B. -2 C. 3 D. ﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
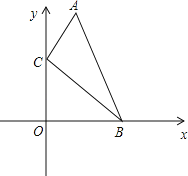
A.(0,0) B.(0,1) C.(0,2) D.(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“绿满鄂南”行动中,某社区计划对面积为1800m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A.5x+4(x+2)=44 B.5x+4(x﹣2)=44 C.9(x+2)=44 D.9(x+2)﹣4×2=44
相关试题

