Question

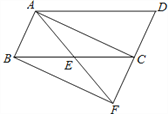
【题目】如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F。

（1）求证：△ABE≌△FCE；

（2）连接AC、BF，若AE＝BC，求证：四边形ABFC为矩形；

（3）在（2）条件下，当△ABC再满足一个什么条件时，四边形ABFC为正方形。

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）当AB＝AC时，矩形ABFC为正方形.

【解析】试题分析：（1）根据平行四边形的性质可得到AB∥CD，从而可得到AB∥DF，根据平行线的性质可得到两组角相等，已知点E是BC的中点，从而可根据AAS来判定△BAE≌△CFE；

（2）根据全等三角形的对应边相等可证得AB=CF．再根据已知可得BC=AF，从而得证；

（3）矩形ABFC要想成为正方形，只只需要一组邻边相等即可，由此可添另条件AB=AC.

试题解析：（1）在 ABCD中，AB∥CD ,AB＝CD，∴ ∠BAE＝∠EFC，

∵ E为BC的中点 ，∴ BE＝EC，

∵ ∠AEB＝∠FEC，∴ △ABE≌△FCE；

（2）由（1）知AB∥CD ， 即 AB∥CF，

∵△ABE≌△FCE ，∴ AB＝FC，

∴ 四边形ABFC为平行四边形 ，∴ AE＝EF＝AF，

∵ AE＝BC ， ∴ BC＝AF ， ∴ABFC是矩形；

（3）当△ABC为等腰三角形时，即 AB＝AC时，矩形ABFC为正方形.