【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
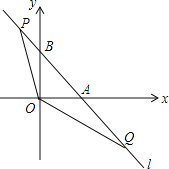
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于![]() ,求二次项系数a的值.
,求二次项系数a的值.
参考答案:
【答案】(1)△AOB周长为2+![]() .(2)P(﹣
.(2)P(﹣![]() ,1+
,1+![]() ).(3)a的值为
).(3)a的值为![]() 或﹣2
或﹣2![]() ﹣2.
﹣2.
【解析】
试题分析:(1)先求出A、B坐标,再求出OB、OA、AB即可解决问题.(2)由△PBO∽△OAQ,得![]() =
=![]() ,求出PB,再根据等腰直角三角形性质可以求得点P坐标.(3)先求出m的值,分①a>0,②a<0,两种情形,利用二次函数性质分别求解即可.
,求出PB,再根据等腰直角三角形性质可以求得点P坐标.(3)先求出m的值,分①a>0,②a<0,两种情形,利用二次函数性质分别求解即可.
试题解析:(1)在函数y=﹣x+1中,令x=0,得y=1,
∴B(0,1),
令y=0,得x=1,
∴A(1,0),
则OA=OB=1,AB=![]() ,
,
∴△AOB周长为1+1+![]() =2+
=2+![]() .
.
(2)∵OA=OB,
∴∠ABO=∠BAO=45°,
∴∠PBO=∠QAO=135°,
设∠POB=x,则∠OPB=∠AOQ=135°﹣x﹣90°=45°﹣x,
∴△PBO∽△OAQ,
∴![]() =
=![]() ,
,
∴PB=![]() =
=![]() ,
,
过点P作PH⊥OB于H点,
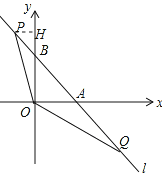
则△PHB为等腰直角三角形,
∵PB=![]() ,
,
∴PH=HB=![]() ,
,
∴P(﹣![]() ,1+
,1+![]() ).
).
(3)由(2)可知△PBO∽△OAQ,若它们的周长相等,则相似比为1,即全等,
∴PB=AQ,
∴![]() =t,
=t,
∵t>0,
∴t=1,
同理可得Q(1+![]() ,﹣
,﹣![]() ),
),
∴m=![]() =
=![]() ﹣1,
﹣1,
∵抛物线经过点A,
∴a+b+c=0,
又∵6a+3b+2c=0,
∴b=﹣4a,c=3a,
对称轴x=2,取值范围![]() ﹣1≤x
﹣1≤x![]() +1,
+1,
①若a>0,则开口向上,
由题意x=![]() ﹣1时取得最大值
﹣1时取得最大值![]() =2
=2![]() +2,
+2,
即(![]() ﹣1)2a+(
﹣1)2a+(![]() ﹣1)b+c=2
﹣1)b+c=2![]() +2,
+2,
解得a=![]() .
.
②若a<0,则开口向下,
由题意x=2时取得最大值2![]() +2,
+2,
即4a+2b+c=2![]() +2,
+2,
解得a=﹣2![]() ﹣2.
﹣2.
综上所述所求a的值为![]() 或﹣2
或﹣2![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
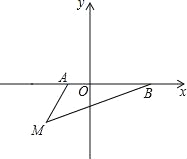
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=
 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,广州市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,比第二档的单价每千瓦时提高0.05元. 海珠区的李白同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的另一位居民杜甫家今年4、5月份的家庭用电量分别为200和 490千瓦时,请你依据题目条件,计算杜甫家4、8月份的电费分别为多少元?
-
科目: 来源: 题型:
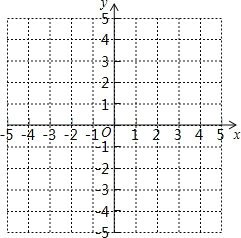
查看答案和解析>>【题目】已知在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,4),B(1,1),C(3,2).
(1)画出△ABC
(2)将△ABC先向左平移3个单位长度,再向下平移4个单位长度得到△A1B1C1,请写出A1,B1,C1三个点的坐标,并在图上画出△A1B1C1;
(3)求出线段BC在第(2)问的平移过程扫过的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中,属于命题的是( )
A.等角的余角相等
B.两点之间,线段最短吗
C.连接P、Q两点
D.花儿会不会在春天开放 -
科目: 来源: 题型:
查看答案和解析>>【题目】点到直线的距离是指这点到这条直线的
A、垂线段B、垂线的长
C、长度D、垂线段的长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

相关试题

