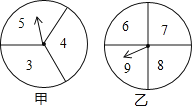
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
参考答案:
【答案】(1)共有12种等可能性;(2)![]() ;
;![]()
【解析】
试题分析:(1)根据题意列出表格,得出游戏中两数和的所有可能的结果数;
(2)根据(1)得出两数和共有的情况数和其中和小于12的情况、和大于12的情况数,再根据概率公式即可得出答案.
试题解析:(1)根据题意列表如下:
甲 乙 | 6 | 7 | 8 | 9 |
3 | 9 | 10 | 11 | 12 |
4 | 10 | 11 | 12 | 13 |
5 | 11 | 12 | 13 | 14 |
可见,两数和共有12种等可能性;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为![]() ;
;
刘凯获胜的概率为![]()
-
科目: 来源: 题型:
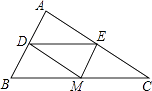
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是cm.
-
科目: 来源: 题型:
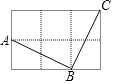
查看答案和解析>>【题目】在由6个大小相同的小正方形组成的方格中;如图,A、B、C是三个格点(即小正方形的顶点).判断AB与BC的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x+y=7,用x的代数式表示y,则y=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
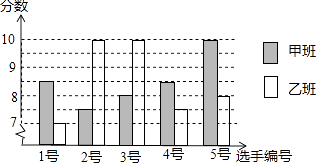
(1)根据上图填写下表:平均数
中位数
众数
方差
甲班
8.5
8.5
乙班
8.5
10
1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O.
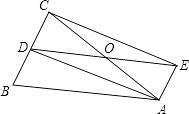
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

相关试题

