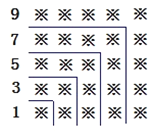
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
参考答案:
【答案】(1)100,10;(2)n2;(3)2419
【解析】
(1)观察已知式子可知,从1 开始的连续奇数的和等于这些奇数的个数的平方,根据规律解答即可;
(2)根据(1)中观察的规律写出结论即可;
(2)利用(2)的结论计算即可.
(1)∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
∴1+3+5+7+9+…+19=(19+1)×5=100=10;
故答案为:100,10.
(2)由(1)可得
1+3+5+7+9+…+(2n-1)= n2;
故答案为:n2;
(3)19+21+23+25+27+…+99
=502-92
=2419.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )

A.2
B. ﹣
﹣  π
π
C.1
D. +
+  π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如下:
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下
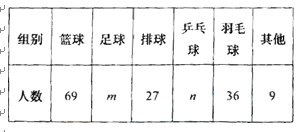

(1)请你写出统计表中空缺部分的人数m= , n= .
(2)在扇形统计图中,羽毛球所对应的扇形圆心角等于 .
(3)请你根据调查结果,给小强部长简要提出两条合理化的建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()
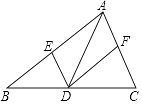
A.若AD⊥BC,则四边形AEDF是矩形
B.若AD垂直平分BC,则四边形AEDF是矩形
C.若BD=CD,则四边形AEDF是菱形
D.若AD平分∠BAC,则四边形AEDF是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=
 ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

-
科目: 来源: 题型:
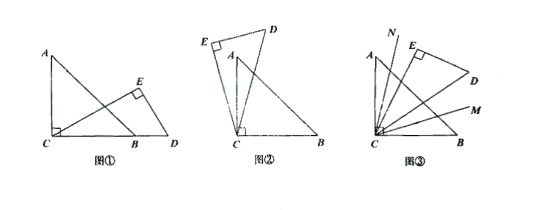
查看答案和解析>>【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
相关试题

