搜索
【题目】如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）
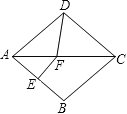
A.50°B.60°C.70°D.80°
参考答案：
【答案】B
【解析】
如图，连接BF，
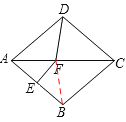
在菱形ABCD中，∵∠BAD=80°，
∴∠BAC=
∠BAD=×80°=40°，∠BCF=∠DCF，BC=CD，
∠ABC=180°﹣∠BAD=180°﹣80°=100°．
∵EF是线段AB的垂直平分线，∴AF=BF，∠ABF=∠BAC=40°．
∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°．
∵在△BCF和△DCF中，BC=CD，∠BCF=∠DCF，CF=CF，∴△BCF≌△DCF（SAS）．
∴∠CDF=∠CBF=60°．故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2m，喷出水流的运动路线是抛物线. 如果水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3.6m，求水流的落地点C到水枪底部B的距离.
-
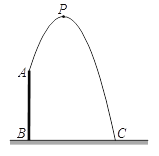
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
是⊙O的直径，点
是
的中点，连接
并延长至点
，使
，点
是
上一点，且
， 
的延长线交
的延长线于点
， 
交⊙O于点
，连接
.（1）求证：
是⊙O的切线；（2）当
时，求
的长.
-
科目： 来源： 题型：
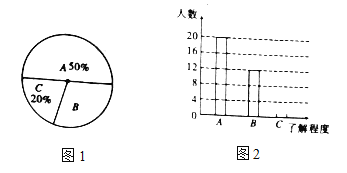
查看答案和解析>>【题目】为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
（1）求该班共有多少名学生；
（2）在条形图中，将表示“一般了解”的部分补充完整；
（3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；
（4）如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点E是矩形ABCD边AB上一动点（不与点B重合），过点E作EF⊥DE交BC于点F，连接DF．已知AB = 4cm，AD = 2cm，设A，E两点间的距离为xcm，△DEF面积为ycm2．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整：
（1）确定自变量x的取值范围是 ；
（2）通过取点、画图、测量、分析，得到了x与y的几组值，如下表：
x/cm
0
0.5
1
1.5
2
2.5
3
3.5
…
y/cm2
4.0
3.7
3.9
3.8
3.3
2.0
…
（说明：补全表格时相关数值保留一位小数）
（3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（4）结合画出的函数图象，解决问题：当△DEF面积最大时，AE的长度为 cm．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共180件其进价和售价如表：（注：获利=售价进价）
（1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
（2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案.
-
科目： 来源： 题型：
查看答案和解析>>【题目】求不等式（2x﹣1）（x+3）＞0的解集．
解：根据“同号两数相乘，积为正”可得：①
或 ②
．解①得x＞
；解②得x＜﹣3．∴不等式的解集为x＞
或x＜﹣3．请你仿照上述方法解决下列问题：
（1）求不等式（2x﹣3）（x+1）＜0的解集．
（2）求不等式
≥0的解集．
相关试题
